Decision Trees
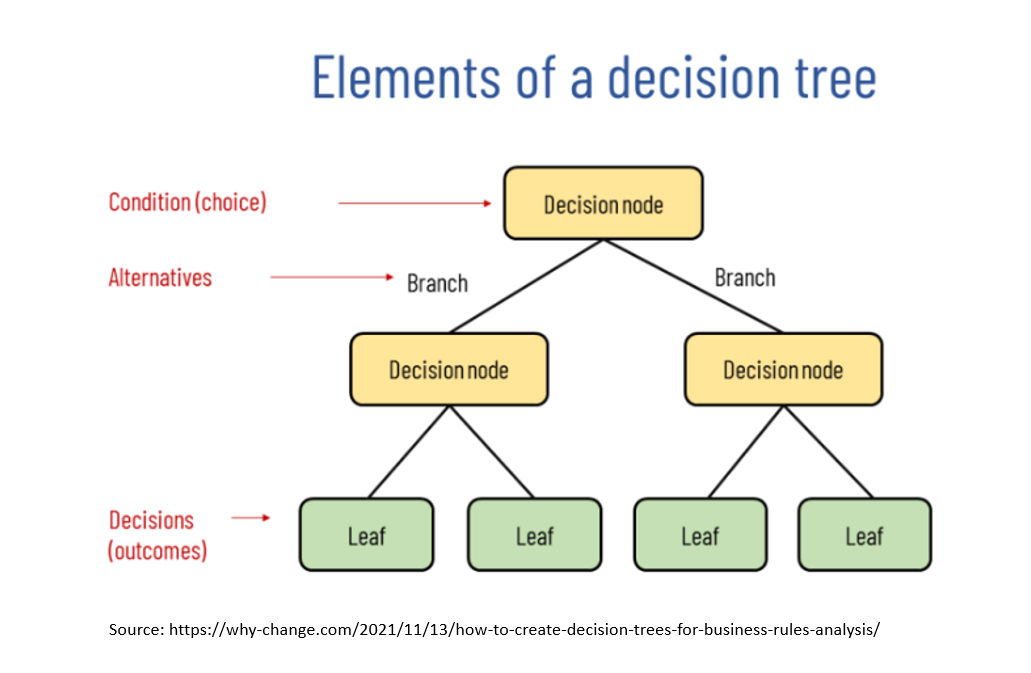
A decision tree is a predictive modeling technique used in machine learning and data mining to model decisions and their possible consequences. It is a tree-like model where internal nodes represent tests on attributes, branches represent the possible outcomes of these tests, and leaf nodes represent the final decision or outcome.
The basic idea behind the decision tree is to divide the dataset into smaller and smaller subsets based on the values of the input features until each subset contains only instances of a single class (for classification) or a single predicted value (for regression). This process is called recursive partitioning and is done by selecting the best feature to split the data at each tree node.
The best feature selection to split the data is made using a metric such as information gain or Gini impurity, which measures the reduction in entropy or impurity in the target variable that results from splitting the data on a particular feature. The feature with the highest information gain or lowest Gini impurity is selected as the split criterion.
Once a feature is selected, the data is split into two or more subsets, each corresponding to a particular feature value. This process is repeated recursively for each subset until the stopping criterion is met (e.g., a minimum number of instances per leaf node is reached).
During the prediction phase, a new input is traversed through the decision tree, starting at the root node and following the tree’s path based on the input features’ values. The final prediction is then made by the leaf node that the input reaches.
Advantages and Disadvantages of Decision Trees
Decision trees have several advantages and disadvantages:
Advantages:
Easy to understand and interpret: Decision trees are intuitive and easy to understand, even for non-experts. They can be visualized and explained quickly.
Non-parametric: Decision trees do not require assumptions about the underlying distribution of the data, making them useful for both linear and nonlinear relationships.
Can handle both numerical and categorical data: Decision trees can handle both numerical and categorical variables, making them versatile.
Feature selection: Decision trees can be used for feature selection by identifying the most critical variables in the model.
Robust to outliers: Decision trees are robust to outliers and missing data, making them useful for real-world datasets.
Disadvantages:
Overfitting: Decision trees are prone to overfitting, especially with complex or noisy datasets. This can be addressed by using pruning or ensemble methods.
Instability: Small changes in the data can lead to different decision trees, making them unstable.
Bias: Decision trees can be biased towards features with many levels or high cardinality.
Greedy search: The greedy search strategy used by decision trees can lead to suboptimal splits, especially with high-dimensional data.
Limited expressiveness: Decision trees have limited expressiveness compared to other machine learning models, such as neural networks or support vector machines.
Types of Decision Tree
There are several decision tree types, each with its characteristics and use cases. Here are some of the most common types:
Binary decision tree: A binary decision tree is a decision tree where each internal node has two children, and each leaf node represents a class or a predicted value.
Multi-way decision tree: A multi-way decision tree is a type of decision tree where each internal node has three or more children, and each leaf node represents a class or a predicted value.
Regression tree: A regression tree is a decision tree used for regression tasks where the target variable is a continuous value. The split criterion is based on minimizing the variance or the sum of squared errors.
Classification tree: A classification tree is a decision tree used for classification tasks where the target variable is a discrete value or a categorical label. The split criterion is based on maximizing the information gain or minimizing the Gini impurity.
ID3 algorithm: The ID3 algorithm is a classic decision tree algorithm that uses information gain as the split criterion and can handle categorical variables.
C4.5 algorithm: The C4.5 algorithm is an extension of the ID3 algorithm that can handle both categorical and numerical variables and uses the concept of gain ratio to select the best split.
CART algorithm: The CART (Classification and Regression Trees) algorithm is a decision tree algorithm that can handle both classification and regression tasks and uses the Gini impurity or the mean squared error as the split criterion.
Conditional inference tree: A conditional inference tree is a type of decision tree that uses statistical tests to determine the significance of the split and can handle missing values and continuous variables.
Each type of decision tree has its strengths and weaknesses, and the appropriate algorithm’s choice depends on the dataset’s specific characteristics and the task at hand.
Overall, decision trees are a valuable and popular machine learning model, but they have some limitations that should be considered when using them. To address these issues, various techniques such as pruning, ensemble methods (e.g., random forest), and boosting (e.g., gradient boosting) have been developed to improve the performance of decision trees.
YouTube Video
- Visual Guide to Decision Trees
Source: Econoscent
- Decision Tree: Important things to know
Source: Intuitive Machine Learning