Multivariate Analysis of Variance (MANOVA)

Multivariate Analysis of Variance (MANOVA) is a statistical technique used to analyze data that involve multiple dependent variables and one or more independent variables. It is an extension of the univariate analysis of variance (ANOVA), which is used to analyze data that involve a single dependent variable.

MANOVA allows researchers to determine whether there are significant differences among groups on multiple dependent variables simultaneously. This can be useful when studying complex phenomena where multiple variables may be involved in explaining the outcome of interest.

MANOVA is based on the general linear model (GLM) framework and involves estimating a set of linear equations that relate the dependent variables to the independent variables. The technique produces a set of output statistics, including F-values and p-values, that indicate whether there are significant differences among groups on the dependent variables.

In contrast to ANOVA, where we compare individual group means, MANOVA compares the vectors containing the group mean of each dependent variable. MANOVA uses omnibus Wilk’s Lambda, Pillai’s Trace (most robust to departures from assumptions), Roy’s Largest Root, or Hotelling-Lawley’s test, which are later converted to F statistics for assessing the significance of the group differences. Pillai’s Trace has the highest statistical power. MANOVA maximizes the discrimination in between-groups than within-groups based on best linear combinations of the multiple response variables.

MANOVA analyzes the differences among groups in an independent variable by considering multiple dependent variables. This reduces the type I error which can be inflated by performing separate univariate ANOVA for each dependent variable. MANOVA also controls for inter-correlations among the multiple dependent variables in the dataset. As compared to univariate ANOVA, MANOVA uses more information from the dependent variables i.e., MANOVA may find differences between groups based on combined information from the multiple dependent variables.

MANOVA follows similar assumptions as in ANOVA for the independence of observations and homogeneity of variances

Data

Suppose we have a data set of different landuse (NLCD) and with SOC and NDVI, We want to see if SOC and NDVI are associated with different NLCD using MANOVA.

gp_soil_data.csv

Code

library(tidyverse)
# define data folder
urlfile = "https://github.com//zia207/r-colab/raw/main/Data/USA/gp_soil_data.csv"
mf<-read_csv(url(urlfile))

Get summary statistics based on each dependent variable:

Code

# summary statistics for dependent variable height 
mf %>% group_by(NLCD) %>%  summarise(n = n(), mean = mean(SOC), sd = sd(SOC))

# A tibble: 4 × 4
  NLCD                   n  mean    sd
  <chr>              <int> <dbl> <dbl>
1 Forest                93 10.4   6.80
2 Herbaceous           150  5.48  3.93
3 Planted/Cultivated    97  6.70  3.60
4 Shrubland            127  4.13  3.74

Code

# summary statistics for dependent variable canopy_vol 
mf %>% group_by(NLCD) %>%  summarise(n = n(), mean = mean(NDVI), sd = sd(NDVI))

# A tibble: 4 × 4
  NLCD                   n  mean    sd
  <chr>              <int> <dbl> <dbl>
1 Forest                93 0.571 0.116
2 Herbaceous           150 0.400 0.131
3 Planted/Cultivated    97 0.533 0.121
4 Shrubland            127 0.308 0.130

Code

#| fig.width: 8
#| fig.height: 5

# SOC
p1 <- ggplot(mf, aes(x = NLCD, y = SOC, fill = NLCD)) +
  geom_boxplot(outlier.shape = NA) + 
  theme(legend.position="none")+
  ggtitle("SOC vs NLCD") 

# NDVI
p2 <- ggplot(mf, aes(x = NLCD, y = NDVI, fill = NLCD)) + 
  geom_boxplot(outlier.shape = NA) + 
  theme(legend.position="none") +
  ggtitle("NDVI vs NLCD")

Code

library(patchwork)
p1+p2

Perform one-way MANOVA

In R, the manova function is used to perform a Multivariate Analysis of Variance (MANOVA). The syntax for the manova function is as follows:

Code

dep_vars <- cbind(mf$SOC, mf$NDVI)
fit <- manova(dep_vars ~ NLCD, data = mf)

Interpretation of output of MANOVA

The output of manova function is useful for testing whether there are significant differences between groups on multiple dependent variables. It is also useful for investigating the direction and magnitude of the effects.

Code

summary(fit)

           Df  Pillai approx F num Df den Df    Pr(>F)    
NLCD        3 0.45615   45.599      6    926 < 2.2e-16 ***
Residuals 463                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The Pillai’s Trace test statistics is statistically significant [Pillai’s Trace = 0.4561, F(6, 926) = 45.599, p < 0.001] and indicates that NLCD have a statistically significant association with both combined SOC and NDVI.

Code

# get effect size
library(effectsize)
effectsize::eta_squared(fit)

# Effect Size for ANOVA (Type I)

Parameter | Eta2 (partial) |       95% CI
-----------------------------------------
NLCD      |           0.23 | [0.19, 1.00]

- One-sided CIs: upper bound fixed at [1.00].

The measure of effect size (Partial Eta Squared; ηp2) is 0.23 and suggests that there is a moderte effect of NLCD on both SOC and NDVI.

Post-hoc test of MANOVA

The MANOVA results suggest that there are statistically significant (p < 0.001) differences between NLCD, but it does not tell which NLCD are different from each other. To know which NLCD are significantly different, the post-hoc test needs to carry out.

To test the between-group differences, the univariate ANOVA can be done on each dependent variable, but this will be not appropriate and lose information that can be obtained from multiple variables together.

Linear discriminant analysis (LDA) is useful to show the differences between each group. LDA will discriminate the groups using information from both the dependent variables

Note

Discriminant analysis is a statistical method used to determine whether a set of variables can be used to classify observations into predefined groups. The goal of discriminant analysis is to build a predictive model that uses a set of predictor variables to classify new observations into one of several predefined groups. This can be used to understand the differences between groups, to identify the most important variables in predicting group membership, and to develop a classification rule that can be used to classify new observations.

There are two types of discriminant analysis: linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA)

Discriminant analysis is commonly used for classification problems in which the classes are well-defined and the data are normally distributed. It can be used for both binary classification (i.e., separating two groups) and multi-class classification (i.e., separating more than two groups). It can also be used for feature selection, to identify the most important variables in predicting group membership.

lda() function of MASS package to do Linear Discriminant Analysis of group variables:

Code

library(MASS)
post_hoc <- lda(mf$NLCD ~ dep_vars, CV=F)
post_hoc

Call:
lda(mf$NLCD ~ dep_vars, CV = F)

Prior probabilities of groups:
            Forest         Herbaceous Planted/Cultivated          Shrubland 
         0.1991435          0.3211991          0.2077088          0.2719486 

Group means:
                   dep_vars1 dep_vars2
Forest             10.430882 0.5705648
Herbaceous          5.476967 0.4003461
Planted/Cultivated  6.696722 0.5332255
Shrubland           4.130764 0.3083878

Coefficients of linear discriminants:
                  LD1       LD2
dep_vars1 -0.01809082 -0.250882
dep_vars2 -7.60110166  4.955480

Proportion of trace:
   LD1    LD2 
0.9167 0.0833

We can plot LD1 and LD2 to visualize discrimination of two predicted lda values:

Code

# create dataframe
plot_lda <- data.frame(mf[, "NLCD"], lda = predict(post_hoc)$x)
# plot
ggplot(plot_lda) + 
    geom_point(aes(x = lda.LD1, y = lda.LD2, colour =NLCD), size = 4)

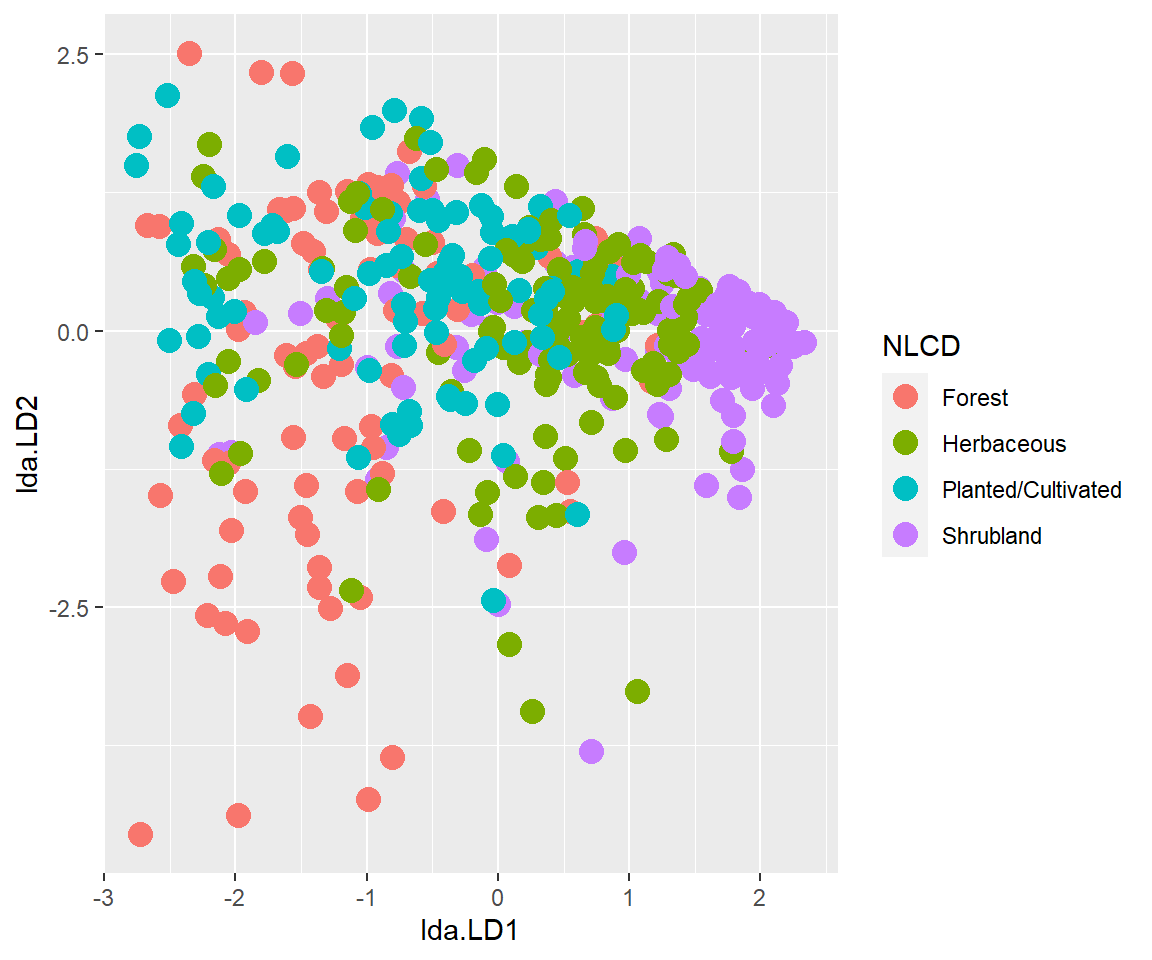
The LDA scatter plot discriminates against NLCDs based on the two dependent variables. The Forest and Shurbland has a significant difference (well separated) as compared to Herbaceous and Planted/Cultivated land.

# Multivariate Analysis of Variance (MANOVA) {.unnumbered} Multivariate Analysis of Variance (MANOVA) is a statistical technique used to analyze data that involve multiple dependent variables and one or more independent variables. It is an extension of the univariate analysis of variance (ANOVA), which is used to analyze data that involve a single dependent variable. MANOVA allows researchers to determine whether there are significant differences among groups on multiple dependent variables simultaneously. This can be useful when studying complex phenomena where multiple variables may be involved in explaining the outcome of interest. MANOVA is based on the general linear model (GLM) framework and involves estimating a set of linear equations that relate the dependent variables to the independent variables. The technique produces a set of output statistics, including F-values and p-values, that indicate whether there are significant differences among groups on the dependent variables. In contrast to ANOVA, where we compare individual group means, MANOVA compares the vectors containing the group mean of each dependent variable. MANOVA uses omnibus Wilk's Lambda, Pillai's Trace (most robust to departures from assumptions), Roy's Largest Root, or Hotelling-Lawley's test, which are later converted to F statistics for assessing the significance of the group differences. Pillai's Trace has the highest statistical power. MANOVA maximizes the discrimination in between-groups than within-groups based on best linear combinations of the multiple response variables. MANOVA analyzes the differences among groups in an independent variable by considering multiple dependent variables. This reduces the type I error which can be inflated by performing separate univariate ANOVA for each dependent variable. MANOVA also controls for inter-correlations among the multiple dependent variables in the dataset. As compared to univariate ANOVA, MANOVA uses more information from the dependent variables i.e., MANOVA may find differences between groups based on combined information from the multiple dependent variables. MANOVA follows similar [assumptions as in ANOVA](https://www.statisticalaid.com/one-way-anova-using-r/) for the independence of observations and homogeneity of variances Data Suppose we have a data set of different landuse (NLCD) and with SOC and NDVI, We want to see if SOC and NDVI are associated with different NLCD using MANOVA. [gp_soil_data.csv](https://www.dropbox.com/s/9ikm5yct36oflei/gp_soil_data.csv?dl=0) ```{r} #| warning: false #| error: false library(tidyverse) # define data folder urlfile = "https://github.com//zia207/r-colab/raw/main/Data/USA/gp_soil_data.csv" mf<-read_csv(url(urlfile)) ``` Get summary statistics based on each dependent variable: ```{r} #| warning: false #| error: false # summary statistics for dependent variable height mf %>% group_by(NLCD) %>% summarise(n = n(), mean = mean(SOC), sd = sd(SOC)) ``` ```{r} #| warning: false #| error: false # summary statistics for dependent variable canopy_vol mf %>% group_by(NLCD) %>% summarise(n = n(), mean = mean(NDVI), sd = sd(NDVI)) ``` ```{r} #| warning: false #| error: false #| fig.width: 8 #| fig.height: 5 # SOC p1 <- ggplot(mf, aes(x = NLCD, y = SOC, fill = NLCD)) + geom_boxplot(outlier.shape = NA) + theme(legend.position="none")+ ggtitle("SOC vs NLCD") # NDVI p2 <- ggplot(mf, aes(x = NLCD, y = NDVI, fill = NLCD)) + geom_boxplot(outlier.shape = NA) + theme(legend.position="none") + ggtitle("NDVI vs NLCD") ``` ```{r} #| warning: false #| error: false #| fig.width: 10 #| fig.height: 4 library(patchwork) p1+p2 ``` ### Perform one-way MANOVA In R, the manova function is used to perform a Multivariate Analysis of Variance (MANOVA). The syntax for the manova function is as follows: ```{r} #| warning: false #| error: false dep_vars <- cbind(mf$SOC, mf$NDVI) fit <- manova(dep_vars ~ NLCD, data = mf) ``` #### Interpretation of output of MANOVA The output of manova function is useful for testing whether there are significant differences between groups on multiple dependent variables. It is also useful for investigating the direction and magnitude of the effects. ```{r} #| warning: false #| error: false summary(fit) ``` The Pillai's Trace test statistics is statistically significant \[Pillai's Trace = 0.4561, F(6, 926) = 45.599, p \< 0.001\] and indicates that NLCD have a statistically significant association with both combined SOC and NDVI. ```{r} #| warning: false #| error: false # get effect size library(effectsize) effectsize::eta_squared(fit) ``` The measure of effect size (Partial Eta Squared; ηp2) is 0.23 and suggests that there is a moderte effect of NLCD on both SOC and NDVI. ### Post-hoc test of MANOVA The MANOVA results suggest that there are statistically significant (p \< 0.001) differences between NLCD, but it does not tell which NLCD are different from each other. To know which NLCD are significantly different, the post-hoc test needs to carry out. To test the between-group differences, the univariate ANOVA can be done on each dependent variable, but this will be not appropriate and lose information that can be obtained from multiple variables together. Linear discriminant analysis (LDA) is useful to show the differences between each group. LDA will discriminate the groups using information from both the dependent variables ::: callout-note Discriminant analysis is a statistical method used to determine whether a set of variables can be used to classify observations into predefined groups. The goal of discriminant analysis is to build a predictive model that uses a set of predictor variables to classify new observations into one of several predefined groups. This can be used to understand the differences between groups, to identify the most important variables in predicting group membership, and to develop a classification rule that can be used to classify new observations. There are two types of discriminant analysis: linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA) Discriminant analysis is commonly used for classification problems in which the classes are well-defined and the data are normally distributed. It can be used for both binary classification (i.e., separating two groups) and multi-class classification (i.e., separating more than two groups). It can also be used for feature selection, to identify the most important variables in predicting group membership. ::: lda() function of MASS package to do Linear Discriminant Analysis of group variables: ```{r} #| warning: false #| error: false library(MASS) post_hoc <- lda(mf$NLCD ~ dep_vars, CV=F) post_hoc ``` We can plot LD1 and LD2 to visualize discrimination of two predicted lda values: ```{r} #| warning: false #| error: false #| fig.width: 6 #| fig.height: 5 # create dataframe plot_lda <- data.frame(mf[, "NLCD"], lda = predict(post_hoc)$x) # plot ggplot(plot_lda) + geom_point(aes(x = lda.LD1, y = lda.LD2, colour =NLCD), size = 4) ``` The LDA scatter plot discriminates against NLCDs based on the two dependent variables. The Forest and Shurbland has a significant difference (well separated) as compared to Herbaceous and Planted/Cultivated land. ### Further Reading 1. [MANOVA(Multivariate Analysis of Variance) using R](https://www.r-bloggers.com/2021/11/manovamultivariate-analysis-of-variance-using-r/) 2.