2. Logistic Regression (Binary Classification)

This tutorial will focus on implementing a logistic model in R, a powerful open-source statistical software that provides numerous functions for easily fitting, interpreting, and visualizing these models. We will begin by reviewing the fundamentals of logistic models, which include understanding their structure, key components, and the types of data they are best suited to handle.

My approach will be step-by-step, starting with constructing a logistic model using synthetic data without relying on any built-in R packages. We will then demonstrate how to fit a logistic model using R’s built-in functions (glm), interpret the model outputs, evaluate model performance, and visualize the results using different R packages.

Overview

Logistic regression is a statistical method useful in scenarios where the categorical outcome variable has only two possible classes. It is a binary classification method that predicts the probability of an instance belonging to a particular category or class. The method derives its name from its use of the logistic function to model the probability of a given class.

Logistic regression falls under the category of supervised learning. This means that it makes predictions based on labeled data. The method is widely used in various fields, such as finance, healthcare, and marketing. Logistic regression is particularly useful in analyzing datasets with many variables and can be used to identify significant variables that influence the outcome variable.

Despite its name, logistic regression is not used for regression but rather for classification. It is a powerful tool that can help businesses and researchers make informed decisions based on the probability of an event occurring.

The goal of logistic regression is to model the probability \(P(Y = 1 \mid \mathbf{X})\) of a binary response variable \(Y\), where \(Y \in \{0, 1\}\).

The logistic regression model is written as:

\[ P(Y = 1 \mid \mathbf{X}) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p)}} \]

This is equivalent to:

\[ \text{logit}(P) = \ln\left(\frac{P}{1 - P}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_p X_p \]

where:

• \(\text{logit}(P)\): The log-odds of \(P(Y = 1)\)

• \(\beta_0\): The intercept.

• \(\beta_1, \beta_2, \dots, \beta_p\): Coefficients for predictors \(X_1, X_2, \dots, X_p\)

The logistic regression model is estimated using maximum likelihood estimation (MLE). For each observation ( i ), the probability of observing \(Y_i\) given \(\mathbf{X}_i\) is:

\[ P(Y_i \mid \mathbf{X}_i) = \hat{p}_i^{Y_i} \cdot (1 - \hat{p}_i)^{1 - Y_i} \]

where

\(\hat{p}_i = P(Y_i = 1 \mid \mathbf{X}_i)\).

The likelihood function for all \(n\) observations is:

\[ L(\boldsymbol{\beta}) = \prod_{i=1}^n P(Y_i \mid \mathbf{X}_i)\]

Taking the log to simplify computation, we get the log-likelihood:

\[ \ell(\boldsymbol{\beta}) = \sum_{i=1}^n \left[ Y_i \ln(\hat{p}_i) + (1 - Y_i) \ln(1 - \hat{p}_i) \right] \]

The coefficients \(\boldsymbol{\beta} = (\beta_0, \beta_1, \dots, \beta_p)\) are estimated by maximizing the log-likelihood:

\[ \hat{\boldsymbol{\beta}} = \arg\max_{\boldsymbol{\beta}} \ell(\boldsymbol{\beta}) \]

This is typically done using numerical optimization techniques such as Iterative Reweighted Least Squares (IRLS), which is employed by the glm() function.

• Each coefficient \(\beta_j\) represents the change in the log-odds of \(Y\) for a one-unit increase in \(X_j\), holding other predictors constant:

\[ \ln\left(\frac{P(Y=1 \mid \mathbf{X})}{P(Y=0 \mid \mathbf{X})}\right) = \beta_0 + \beta_1 X_1 + \dots + \beta_j X_j + \dots \]

• In terms of probabilities, the effect of \(X_j\) on \(P(Y=1)\) is non-linear due to the logistic function.

Logistic regression is widely used in various fields, including medicine, finance, and social sciences, for binary classification problems. It can be extended to handle multiclass classification through techniques such as one-vs-rest or one-vs-one.

Logistic Model from Scratch

In this section, we will demonstrate how to build a logistic regression model in R without using any external packages. We will start by generating synthetic data, then proceed to fit the model, compute summary statistics, and validate the model’s performance through k-fold cross-validation. Below are the step-by-step instructions and explanations of the underlying mathematics involved.

Generate Synthetic Data

We need to create a dataset with:

• One binary response variable (contaminated: Yes = 1, No = 0).

• Four linear predictor variables (we’ll call them x1, x2, x3, and x4).

• One categorical variable with two levels (region: highland or lowland).

# Set seed for reproducibility
set.seed(42)

# Generate the covariates
n <- 100
x1 <- rnorm(n, mean = 0, sd = 1)
x2 <- rnorm(n, mean = 0, sd = 1)
x3 <- rnorm(n, mean = 0, sd = 1)
x4 <- rnorm(n, mean = 0, sd = 1)

# Generate the categorical variable
region <- factor(sample(c("highland", "lowland"), n, replace = TRUE))

# Define coefficients
beta_0 <- -1
beta_1 <- 0.5
beta_2 <- -0.3
beta_3 <- 0.2
beta_4 <- 0.1
beta_5 <- 0.7 # Assume this for highland vs lowland effect

# Calculate linear predictor
log_odds <- beta_0 + beta_1 * x1 + beta_2 * x2 + beta_3 * x3 + beta_4 * x4 + beta_5 * (region == "highland")

# Convert to probability using the logistic function
probability <- exp(log_odds) / (1 + exp(log_odds))

# Generate binary response based on probability
contaminated <- rbinom(n, 1, probability)

# Combine into a data frame
data <- data.frame(contaminated = contaminated, x1 = x1, x2 = x2, x3 = x3, x4 = x4, region = region)
head(data)

  contaminated         x1         x2         x3           x4   region
1            0  1.3709584  1.2009654 -2.0009292 -0.004620768  lowland
2            0 -0.5646982  1.0447511  0.3337772  0.760242168  lowland
3            0  0.3631284 -1.0032086  1.1713251  0.038990913  lowland
4            0  0.6328626  1.8484819  2.0595392  0.735072142 highland
5            0  0.4042683 -0.6667734 -1.3768616 -0.146472627  lowland
6            1 -0.1061245  0.1055138 -1.1508556 -0.057887335  lowland

Define the Log-Likelihood Function

To fit a logistic regression without using glm() or any packages, we need to implement maximum likelihood estimation (MLE) from scratch. This involves defining the likelihood function for logistic regression and then using numerical optimization to estimate the coefficients.

Here’s how to do it in R:

The probability that an observation \(Y_i = 1\) (contaminated = Yes) given predictor variables \(X_i\) is given by:

\[ P(Y_i = 1 | X_i) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + \beta_4 x_{i4} + \beta_5 \text{region}_i)}} \] The log-likelihood function for logistic regression, which we want to maximize, is:

\[ \text{log-likelihood} = \sum_{i=1}^n \left( Y_i \cdot \log(P(Y_i = 1 | X_i)) + (1 - Y_i) \cdot \log(1 - P(Y_i = 1 | X_i)) \right) \]

Let’s write this in R, where params will represent the vector of coefficients \(\beta\).

# Define the log-likelihood function
log_likelihood <- function(params, data) {
  # Extract coefficients
  beta_0 <- params[1]
  beta_1 <- params[2]
  beta_2 <- params[3]
  beta_3 <- params[4]
  beta_4 <- params[5]
  beta_5 <- params[6]
  
  # Calculate linear predictor (log-odds)
  log_odds <- beta_0 + beta_1 * data$x1 + beta_2 * data$x2 + 
              beta_3 * data$x3 + beta_4 * data$x4 + 
              beta_5 * (data$region == "highland")
  
  # Calculate probability using the logistic function
  probability <- 1 / (1 + exp(-log_odds))
  
  # Calculate the log-likelihood
  ll <- sum(data$contaminated * log(probability) + 
            (1 - data$contaminated) * log(1 - probability))
  return(-ll)  # Return negative log-likelihood for minimization
}

Optimize the Log-Likelihood Function

We use optim() to find the parameter values that maximize the likelihood (minimizes the negative log-likelihood).

# Initial guesses for coefficients
initial_params <- rep(0, 6)

# Optimize the log-likelihood function
fit <- optim(par = initial_params, fn = log_likelihood, data = data, method = "BFGS")

# Extract the estimated coefficients
estimated_params <- fit$par
estimated_params

[1] -1.1717235  0.4808036 -0.4012342 -0.0907871  0.1267498  0.6483121

Interpret the Results

The estimated_params vector contains our estimated coefficients (\(\beta_0, \beta_1, \ldots, \beta_5\)), which can be interpreted as follows: - Each coefficient represents the effect of the corresponding predictor on the log-odds of contamination. - For example, if estimated_params[2] (the estimate for (\(\beta_1\))) is positive, an increase in x1 increases the log-odds of contamination, and vice versa.

Calculate Summary Statistics of the Model

To calculate standard errors, we can approximate the Hessian matrix (the matrix of second derivatives of the log-likelihood function), which optim() provides if we set hessian = TRUE. The inverse of the Hessian gives the variance-covariance matrix of the estimates.

# Re-run the optimization to get Hessian matrix
fit <- optim(par = initial_params, fn = log_likelihood, data = data, method = "BFGS", hessian = TRUE)

# Extract standard errors from the Hessian matrix
vcov_matrix <- solve(fit$hessian)
standard_errors <- sqrt(diag(vcov_matrix))
standard_errors

[1] 0.3427831 0.2338899 0.2647261 0.2196759 0.2555353 0.4566046

To summarize the results with estimated coefficients and standard errors:

# Combine results in a table
summary_table <- data.frame(
  Coefficient = estimated_params,
  Std_Error = standard_errors,
  Z_value = estimated_params / standard_errors,
  p_value = 2 * (1 - pnorm(abs(estimated_params / standard_errors)))
)

# Display summary table
print(summary_table)

  Coefficient Std_Error    Z_value      p_value
1  -1.1717235 0.3427831 -3.4182654 0.0006302161
2   0.4808036 0.2338899  2.0556834 0.0398130447
3  -0.4012342 0.2647261 -1.5156579 0.1296058904
4  -0.0907871 0.2196759 -0.4132774 0.6794033730
5   0.1267498 0.2555353  0.4960168 0.6198825522
6   0.6483121 0.4566046  1.4198545 0.1556500395

This table gives:

• Coefficient: The estimated (\(\beta\)) values.

• Std. Error: The standard error for each coefficient.

• Z-value: Computed as \(\text{Coefficient} / \text{Std. Error}\).

• p-value: The significance of each coefficient’s effect, testing the null hypothesis that each \(\beta\) is zero.

Odds Ratio (OR)

The odds ratio is a measure commonly used in logistic regression, to quantify the strength of association between two events. It represents the odds of an event occurring in one group compared to the odds of it occurring in another group. The odds ratio is calculated as the exponentiated coefficient of a predictor variable.

The odds ratio helps us understand how a one-unit increase in a predictor variable affects the odds of the outcome. Here’s how to interpret it:

• OR = 1: The predictor does not change the odds of the outcome (no effect).

• OR > 1: The predictor increases the odds of the outcome. For instance, if OR = 1.5, a one-unit increase in the predictor increases the odds of the outcome by 50%.

• OR < 1: The predictor decreases the odds of the outcome. For example, if OR = 0.7, a one-unit increase in the predictor decreases the odds of the outcome by 30%.

odd.ratio<-exp(estimated_params[2:6])
odd.ratio

[1] 1.6173736 0.6694933 0.9132121 1.1351330 1.9123104

Model Performance

Evaluating the performance of a logistic regression model involves several metrics and techniques to understand how well the model predicts the outcome variable (e.g., contaminated vs. not contaminated). Here’s a detailed overview of the key evaluation metrics and methods commonly used in this context:

Confusion Matrix

A confusion matrix is a simple yet powerful tool for evaluating the performance of a classification model. It provides a summary of prediction results on a classification problem. The confusion matrix summarizes:

• True Positives (TP): Correctly predicted positive instances.
• True Negatives (TN): Correctly predicted negative instances.
• False Positives (FP): Incorrectly predicted positive instances (Type I error).
• False Negatives (FN): Incorrectly predicted negative instances (Type II error).

Confusion Matrix Layout:

	Actual Positive (1)	Actual Negative (0)
Predicted Positive (1)	TP	FP
Predicted Negative (0)	FN	TN

#Step 1: Compute Predicted Probabilitie
# Use estimated coefficients to calculate predicted probabilities
predicted_log_odds <- estimated_params[1] + 
                      estimated_params[2] * data$x1 + 
                      estimated_params[3] * data$x2 + 
                      estimated_params[4] * data$x3 + 
                      estimated_params[5] * data$x4 + 
                      estimated_params[6] * (data$region == "highland")

# Convert log-odds to probability
predicted_probabilities <- 1 / (1 + exp(-predicted_log_odds))

#Step 2: Classify Predictions
# Set threshold and classify as 1 if probability > 0.5, else 0
predicted_class <- ifelse(predicted_probabilities > 0.5, 1, 0)
#Step 3: Create the Confusion Matrix
#The confusion matrix compares the actual values of contaminated with the predicted classifications (predicted_class).
actual_class <- data$contaminated
confusion_matrix <- table(Predicted = predicted_class, Actual = actual_class)
confusion_matrix

         Actual
Predicted  0  1
        0 61 23
        1  6 10

Performance Metrics

From the confusion matrix, several performance metrics can be derived:

• Accuracy: The proportion of total correct predictions.

  \[ \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \]

• Precision (Positive Predictive Value): The proportion of predicted positives that are actual positives.

  \[ \text{Precision} = \frac{TP}{TP + FP} \]

• Recall (Sensitivity or True Positive Rate): The proportion of actual positives that are correctly predicted.

\[ \text{Recall} = \frac{TP}{TP + FN} \]

• Specificity (True Negative Rate): The proportion of actual negatives that are correctly predicted.

  \[ \text{Specificity} = \frac{TN}{TN + FP} \]

• F1 Score: The harmonic mean of precision and recall, useful when dealing with imbalanced classes.

  \[ \text{F1 Score} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}} \]

  # define variables
  TP <- confusion_matrix[2, 2]
  TN <- confusion_matrix[1, 1]
  FP <- confusion_matrix[2, 1]
  FN <- confusion_matrix[1, 2]
  
  # accuracy
  accuracy <- (TP + TN) / sum(confusion_matrix)
  
  # precision 
  precision <- TP / (TP + FP)
  
  # Recall 
  recall <- TP / (TP + FN)
  
  # specificity 
  specificity <- TN / (TN + FP)
  
  # f1_score 
  f1_score <- 2 * (precision * recall) / (precision + recall)
  
  # Print the results
  cat("Accuracy:", accuracy, "\n")

  Accuracy: 0.71 

  cat("Precision:", precision, "\n")

  Precision: 0.625 

  cat("Recall:", recall, "\n")

  Recall: 0.3030303 

  cat("Specificity:", specificity, "\n")

  Specificity: 0.9104478 

  cat("F1 Score:", f1_score, "\n")

  F1 Score: 0.4081633 

Receiver Operating Characteristic (ROC) Curve and AUC

The ROC curve is an important tool used in evaluating the performance of a binary classification model. It is a graphical plot that illustrates how well the model can distinguish between positive and negative classes at different threshold settings. The curve displays the trade-off between the true positive rate (sensitivity) and the false positive rate (1 - specificity) as the threshold for classification changes. The true positive rate measures the proportion of actual positive instances that are correctly identified by the model, while the false positive rate measures the proportion of actual negative instances that are incorrectly classified as positive by the model. By analyzing the ROC curve, one can determine the optimal threshold setting that maximizes the true positive rate and minimizes the false positive rate, thereby improving the overall accuracy of the classification model.

• True Positive Rate (TPR): The y-axis represents the true positive rate (sensitivity).
• False Positive Rate (FPR): The x-axis represents the false positive rate.

A typical ROC appears as a line that starts at the bottom left corner (0, 0) and extends towards the top right corner (1, 1). If the curve is closer to the top-left corner, it indicates better performance of the model. A diagonal line from (0, 0) to (1, 1) on the ROC curve represents the performance of a random classifier. A model with perfect discrimination will have an ROC curve passing through the top-left corner, indicating a true positive rate of 1 (sensitivity) and a false positive rate of 0 (specificity). The area under the ROC curve (AUC-ROC) is a widely used summary statistic for quantifying the performance of a classification model. AUC-ROC ranges from 0 to 1, with higher values indicating better discrimination. An AUC-ROC of 0.5 suggests that the model performs no better than random guessing, while an AUC-ROC of 1 indicates perfect classification. To summarize, the ROC curve provides a clear visualization of a classification model’s performance across different threshold settings. This allows users to select an appropriate threshold based on their specific needs for sensitivity and specificity.

The Area Under the Curve (AUC) quantifies the overall ability of the model to discriminate between the positive and negative classes:

• AUC = 1: Perfect discrimination.
• AUC = 0.5: No discrimination (random guessing).

# Calculate and plot ROC Curve
roc_data <- data.frame(probability = predicted_probabilities, actual = actual_class)
roc_data <- roc_data[order(-roc_data$probability), ]
TPR <- cumsum(roc_data$actual) / sum(roc_data$actual)
FPR <- cumsum(1 - roc_data$actual) / sum(1 - roc_data$actual)
AUC <- sum((FPR[-1] - FPR[-length(FPR)]) * (TPR[-1] + TPR[-length(TPR)]) / 2)

# Plot ROC Curve
plot(FPR, TPR, type = 'l', col = 'blue', lwd = 2,
     xlab = 'False Positive Rate (FPR)', 
     ylab = 'True Positive Rate (TPR)',
     main = 'ROC Curve')
abline(a = 0, b = 1, col = 'red', lty = 2)
text(0.6, 0.2, paste("AUC =", round(AUC, 2)), col = 'black', cex = 1.2)

Log-Likelihood and Pseudo-R²

• Log-Likelihood: A measure of how well the model fits the data. Higher values indicate a better fit.

• Pseudo-R²: Various metrics (like McFadden’s R², Cox & Snell R²) can be used to measure the goodness of fit for logistic regression models.

# Function to calculate Log-Likelihood
log_likelihood_value <- function(params, data) {
  beta_0 <- params[1]
  beta_1 <- params[2]
  beta_2 <- params[3]
  beta_3 <- params[4]
  beta_4 <- params[5]
  beta_5 <- params[6]

  # Linear predictor
  log_odds <- beta_0 + beta_1 * data$x1 + beta_2 * data$x2 + 
              beta_3 * data$x3 + beta_4 * data$x4 + 
              beta_5 * (data$region == "highland")

  # Predicted probabilities
  probability <- 1 / (1 + exp(-log_odds))

  # Log-Likelihood calculation
  ll <- sum(data$contaminated * log(probability) + 
            (1 - data$contaminated) * log(1 - probability))
  
  return(ll)  # Return Log-Likelihood
}

# Calculate the log-likelihood using the estimated parameters
ll_value <- log_likelihood_value(estimated_params, data)

# Function to calculate Log-Likelihood of null model
null_model_ll <- function(data) {
  p_null <- mean(data$contaminated)  # Proportion of 1s
  ll_null <- sum(data$contaminated * log(p_null) + 
                 (1 - data$contaminated) * log(1 - p_null))
  return(ll_null)  # Return Log-Likelihood of null model
}

# Calculate Log-Likelihood for null model
ll_null_value <- null_model_ll(data)

# Calculate Pseudo-R²
pseudo_r2 <- 1 - (ll_value / ll_null_value)

# Output the results
cat("Log-Likelihood of the model:", ll_value, "\n")

Log-Likelihood of the model: -58.56622 

cat("Log-Likelihood of the null model:", ll_null_value, "\n")

Log-Likelihood of the null model: -63.41786 

cat("Pseudo-R²:", pseudo_r2, "\n")

Pseudo-R²: 0.07650273 

Cross-Validation

To assess how the model generalizes to an independent dataset, use cross-validation techniques like k-fold cross-validation. This involves splitting the data into \(k\) subsets, training the model on \(k-1\) subsets, and testing it on the remaining subset. This process is repeated \(k\) times, and the performance metrics are averaged.

# Set seed for reproducibility
set.seed(42)

# k-Fold Cross-Validation
k <- 5  # Number of folds
folds <- cut(seq(1, n), breaks = k, labels = FALSE)  # Create folds
metrics <- data.frame(accuracy = numeric(k), precision = numeric(k), recall = numeric(k), f1_score = numeric(k))

for (i in 1:k) {
  # Split data into training and validation sets
  validation_indices <- which(folds == i, arr.ind = TRUE)
  validation_set <- data[validation_indices, ]
  training_set <- data[-validation_indices, ]
  
  # Fit the logistic regression model without using glm
  log_likelihood <- function(params, data) {
    beta_0 <- params[1]
    beta_1 <- params[2]
    beta_2 <- params[3]
    beta_3 <- params[4]
    beta_4 <- params[5]
    beta_5 <- params[6]
    log_odds <- beta_0 + beta_1 * data$x1 + beta_2 * data$x2 + beta_3 * data$x3 + beta_4 * data$x4 + beta_5 * (data$region == "highland")
    probability <- 1 / (1 + exp(-log_odds))
    ll <- sum(data$contaminated * log(probability) + (1 - data$contaminated) * log(1 - probability))
    return(-ll)
  }

  initial_params <- rep(0, 6)
  fit <- optim(par = initial_params, fn = log_likelihood, data = training_set, method = "BFGS", hessian = TRUE)
  estimated_params <- fit$par
  
  # Predict on the validation set
  predicted_log_odds <- estimated_params[1] + estimated_params[2] * validation_set$x1 + 
                        estimated_params[3] * validation_set$x2 + 
                        estimated_params[4] * validation_set$x3 + 
                        estimated_params[5] * validation_set$x4 + 
                        estimated_params[6] * (validation_set$region == "highland")
  predicted_probabilities <- 1 / (1 + exp(-predicted_log_odds))
  predicted_class <- ifelse(predicted_probabilities > 0.5, 1, 0)

  # Create confusion matrix for the current fold
  actual_class <- validation_set$contaminated
  confusion_matrix <- table(Predicted = predicted_class, Actual = actual_class)

  # Calculate performance metrics
  TP <- confusion_matrix[2, 2]  # True Positives
  TN <- confusion_matrix[1, 1]  # True Negatives
  FP <- confusion_matrix[2, 1]  # False Positives
  FN <- confusion_matrix[1, 2]  # False Negatives

  accuracy <- (TP + TN) / sum(confusion_matrix)
  precision <- ifelse(TP + FP == 0, 0, TP / (TP + FP))
  recall <- ifelse(TP + FN == 0, 0, TP / (TP + FN))
  f1_score <- ifelse(precision + recall == 0, 0, 2 * (precision * recall) / (precision + recall))

  # Store the metrics for the current fold
  metrics[i, ] <- c(accuracy, precision, recall, f1_score)
}

# Calculate the average metrics across all folds
average_metrics <- colMeans(metrics)

# Print the results
cat("Average Accuracy:", average_metrics[1], "\n")

Average Accuracy: 0.67 

cat("Average Precision:", average_metrics[2], "\n")

Average Precision: 0.5666667 

cat("Average Recall:", average_metrics[3], "\n")

Average Recall: 0.3304762 

cat("Average F1 Score:", average_metrics[4], "\n")

Average F1 Score: 0.3559019 

# Plot ROC curve
roc_data <- data.frame(probability = predicted_class, actual = actual_class)
roc_data <- roc_data[order(-roc_data$probability), ]
TPR <- cumsum(roc_data$actual) / sum(roc_data$actual)
FPR <- cumsum(1 - roc_data$actual) / sum(1 - roc_data$actual)
AUC <- sum((FPR[-1] - FPR[-length(FPR)]) * (TPR[-1] + TPR[-length(TPR)]) / 2)

# Plot ROC Curve
plot(FPR, TPR, type = 'l', col = 'blue', lwd = 2,
     xlab = 'False Positive Rate (FPR)', 
     ylab = 'True Positive Rate (TPR)',
     main = 'Croos-validated ROC Curve')
abline(a = 0, b = 1, col = 'red', lty = 2)
text(0.6, 0.2, paste("AUC =", round(AUC, 2)), col = 'black', cex = 1.2)

Logistic Model in R

The glm() function in R is commonly used to fit generalized linear models, including logistic regression. Here’s a guide on how to fit a logistic regression model with glm().

Install Required R Packages

Before fitting the logistic model, we need to install and load the necessary R packages. The packages we will use include tidyverse, boot, margins, ggeffects, performance, sjPlot, patchwork, gt, gtsummary, jtools, report, Metrics, metrica, pROC, and ROCR.

# packages list
packages <- c(
  "tidyverse",   # Includes readr, dplyr, ggplot2, etc.
  "plyr",
  "rstatix",
  "boot",
  "margins",
  "marginaleffects",
  "ggeffects",
  "performance",
  "ggpmisc",
  "sjPlot",
  "patchwork",
  "gt",
  "gtsummary",
  "jtools",
  "report",
  "Metrics",
  "metrica",
  "pROC",
    "ROCR"
  )

#| warning: false
#| error: false

# Install missing packages
new_packages <- packages[!(packages %in% installed.packages()[,"Package"])]
if(length(new_packages)) install.packages(new_packages)

# Verify installation
cat("Installed packages:\n")
print(sapply(packages, requireNamespace, quietly = TRUE))

Load R Packages

# Load packages with suppressed messages
invisible(lapply(packages, function(pkg) {
  suppressPackageStartupMessages(library(pkg, character.only = TRUE))
}))

# Check loaded packages
cat("Successfully loaded packages:\n")

Successfully loaded packages:

print(search()[grepl("package:", search())])

 [1] "package:ROCR"            "package:pROC"           
 [3] "package:metrica"         "package:Metrics"        
 [5] "package:report"          "package:jtools"         
 [7] "package:gtsummary"       "package:gt"             
 [9] "package:patchwork"       "package:sjPlot"         
[11] "package:ggpmisc"         "package:ggpp"           
[13] "package:performance"     "package:ggeffects"      
[15] "package:marginaleffects" "package:margins"        
[17] "package:boot"            "package:rstatix"        
[19] "package:plyr"            "package:lubridate"      
[21] "package:forcats"         "package:stringr"        
[23] "package:dplyr"           "package:purrr"          
[25] "package:readr"           "package:tidyr"          
[27] "package:tibble"          "package:ggplot2"        
[29] "package:tidyverse"       "package:stats"          
[31] "package:graphics"        "package:grDevices"      
[33] "package:utils"           "package:datasets"       
[35] "package:methods"         "package:base"           

Data

Our goal is to develop a logistic model to predict paddy soil arsenic class using various irrigation water and soil properties. We have available data of 263 paired groundwater and paddy soil samples from arsenic contaminated areas in Tala Upazilla, Satkhira district, Bangladesh. This data was utilized in on our publication titled “Factors Affecting Paddy Soil Arsenic Concentration in Bangladesh: Prediction and Uncertainty of Geostatistical Risk Mapping” which can be accessed via the this URL.

Full data set is available for download from my Dropbox or from my Github accounts. We will use read_csv() function of readr package to import data as a tidy data.

# Load data
mf<-readr::read_csv("https://github.com/zia207/r-colab/raw/main/Data/Regression_analysis/bd_soil_arsenic.csv")
glimpse(mf)

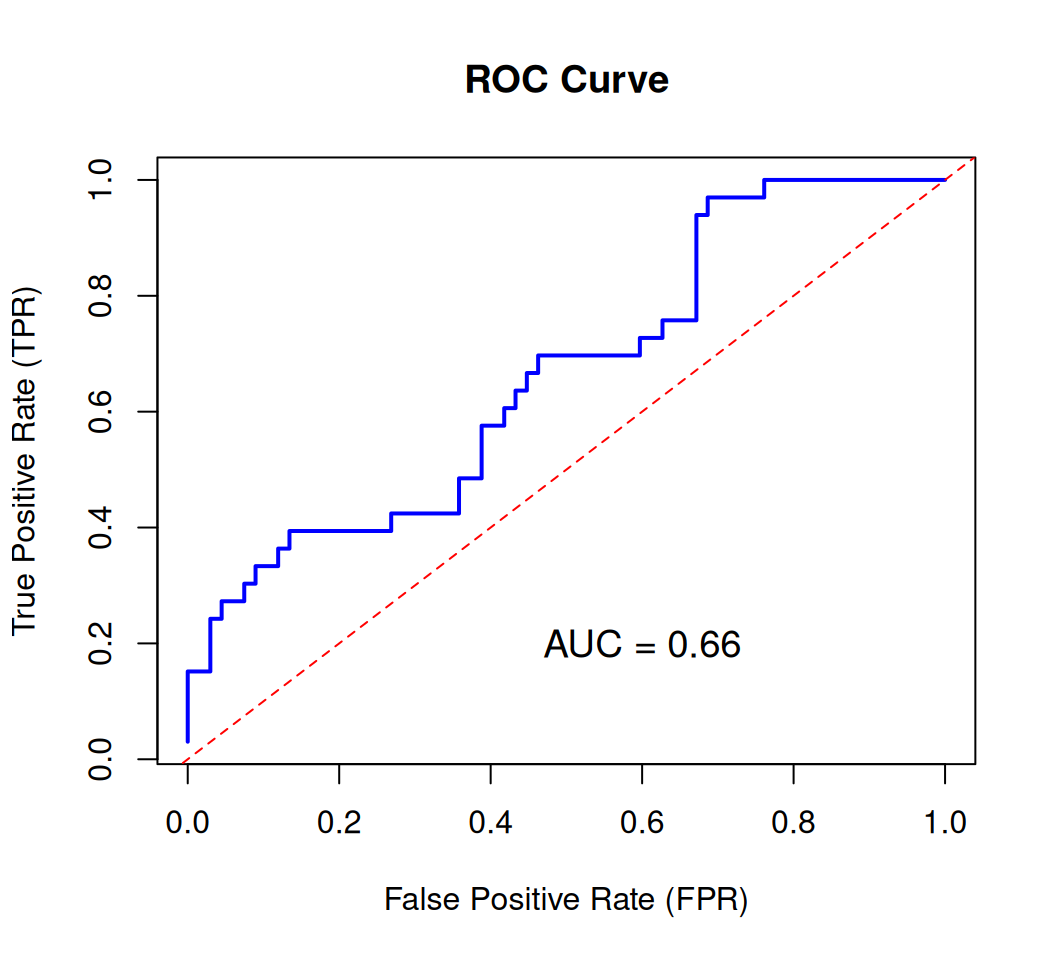
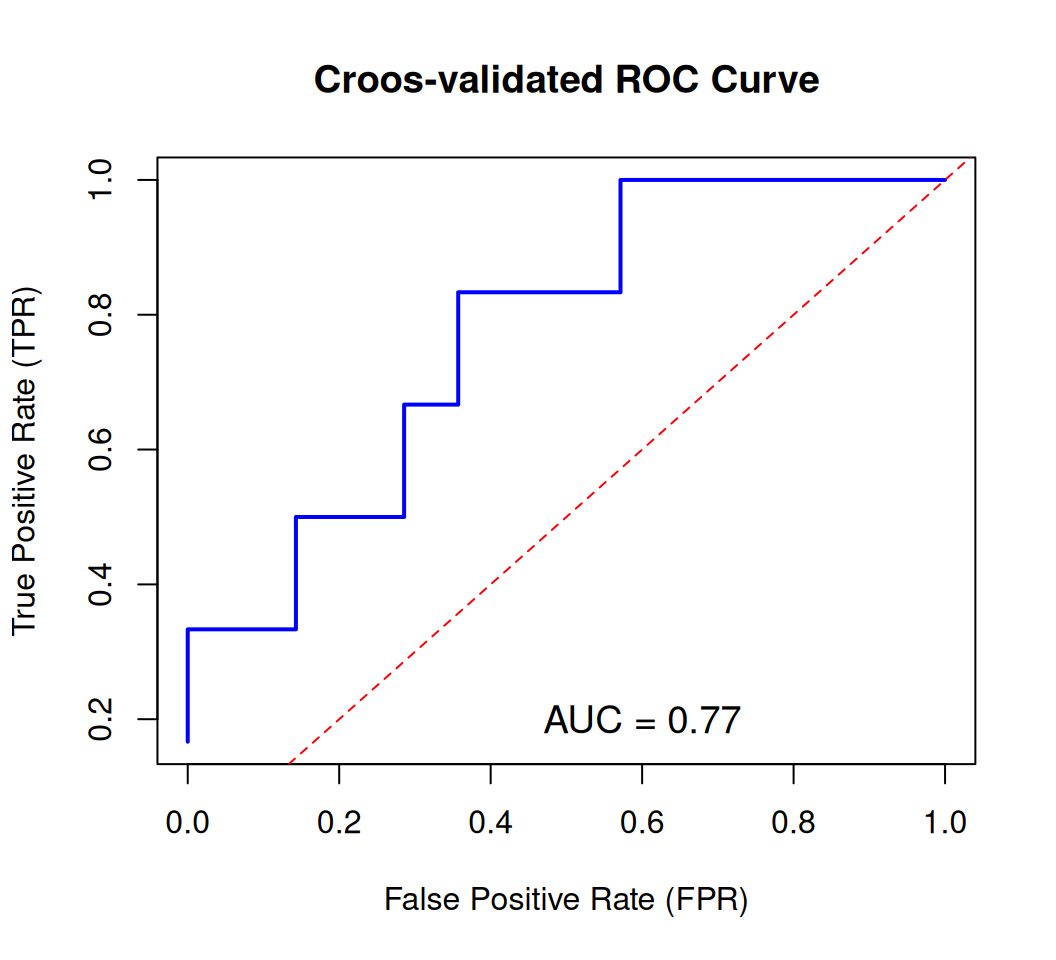
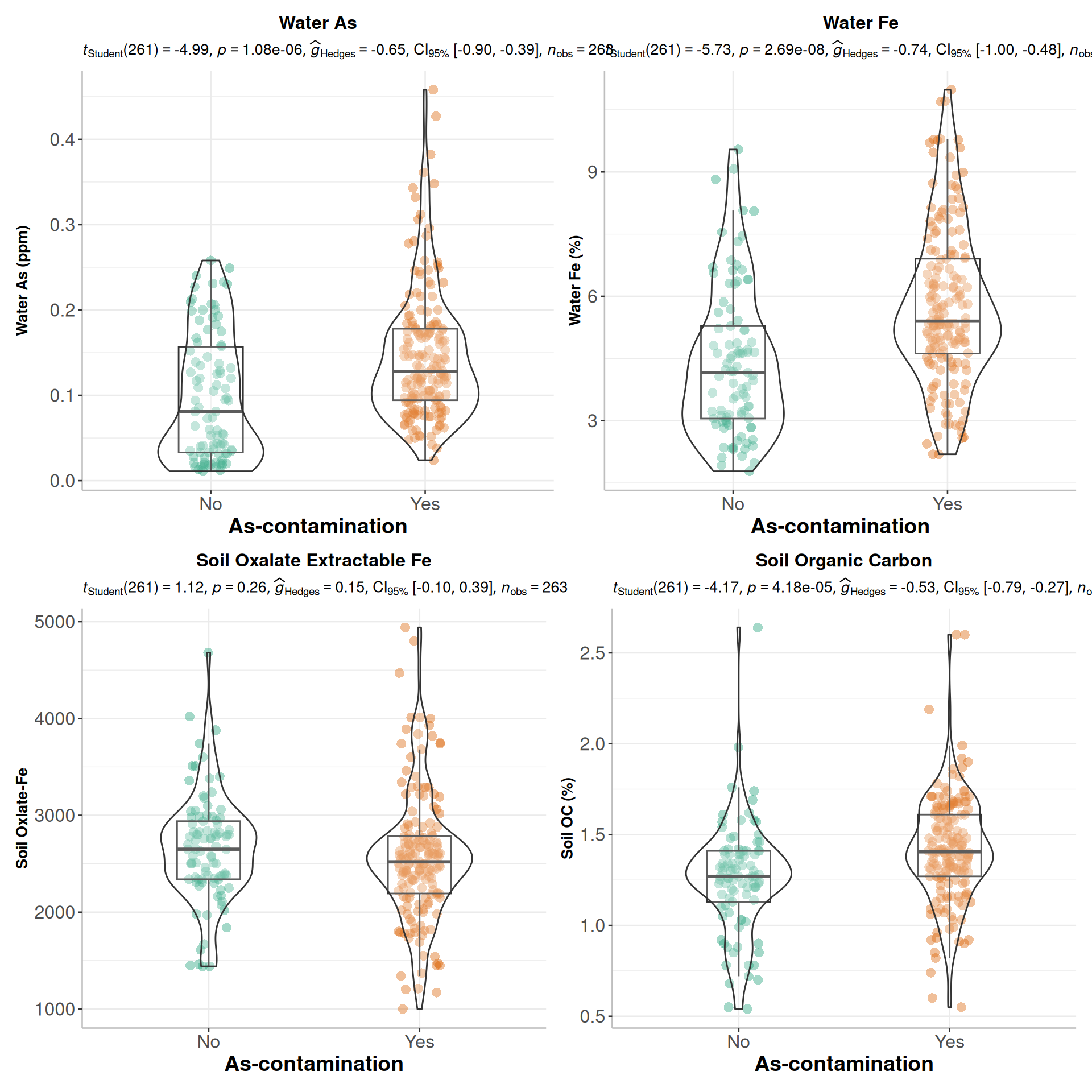
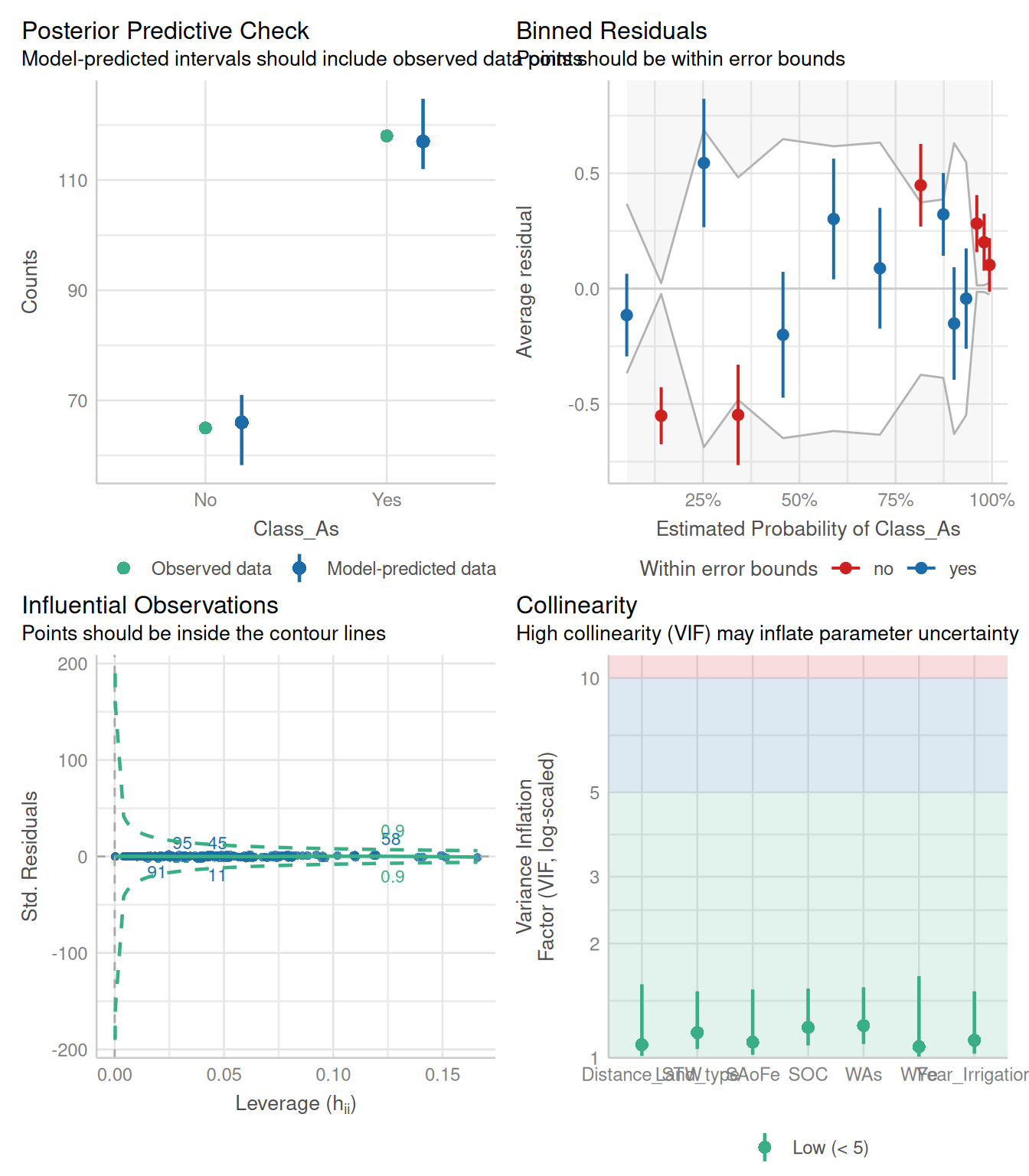
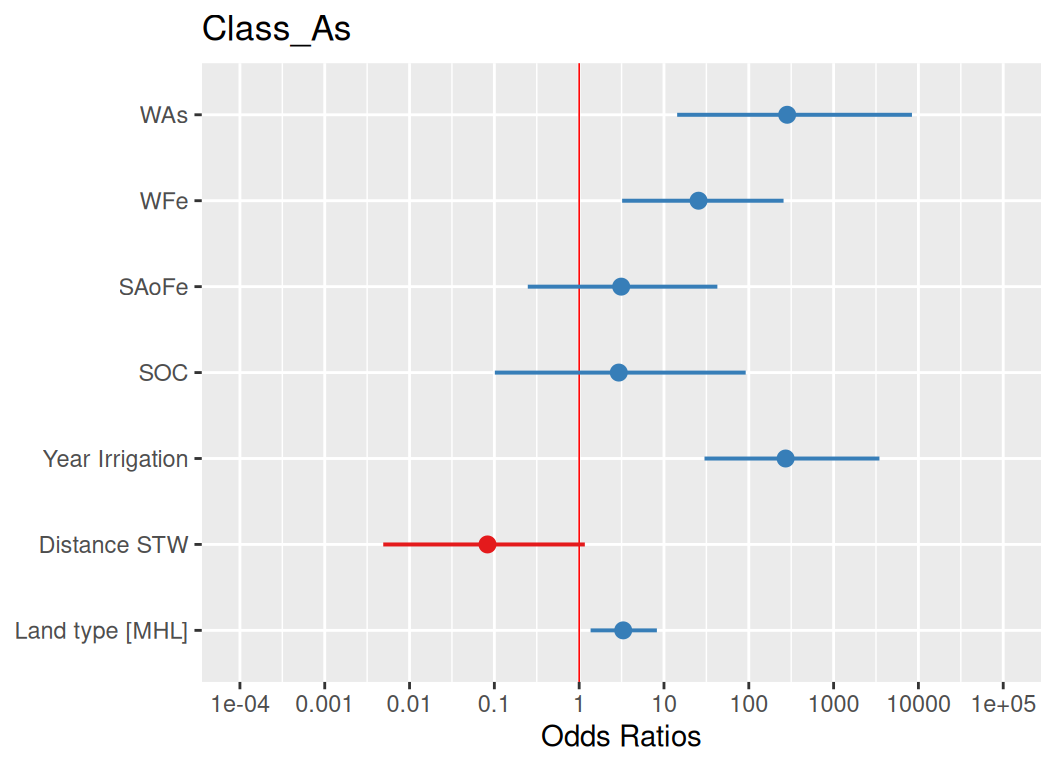
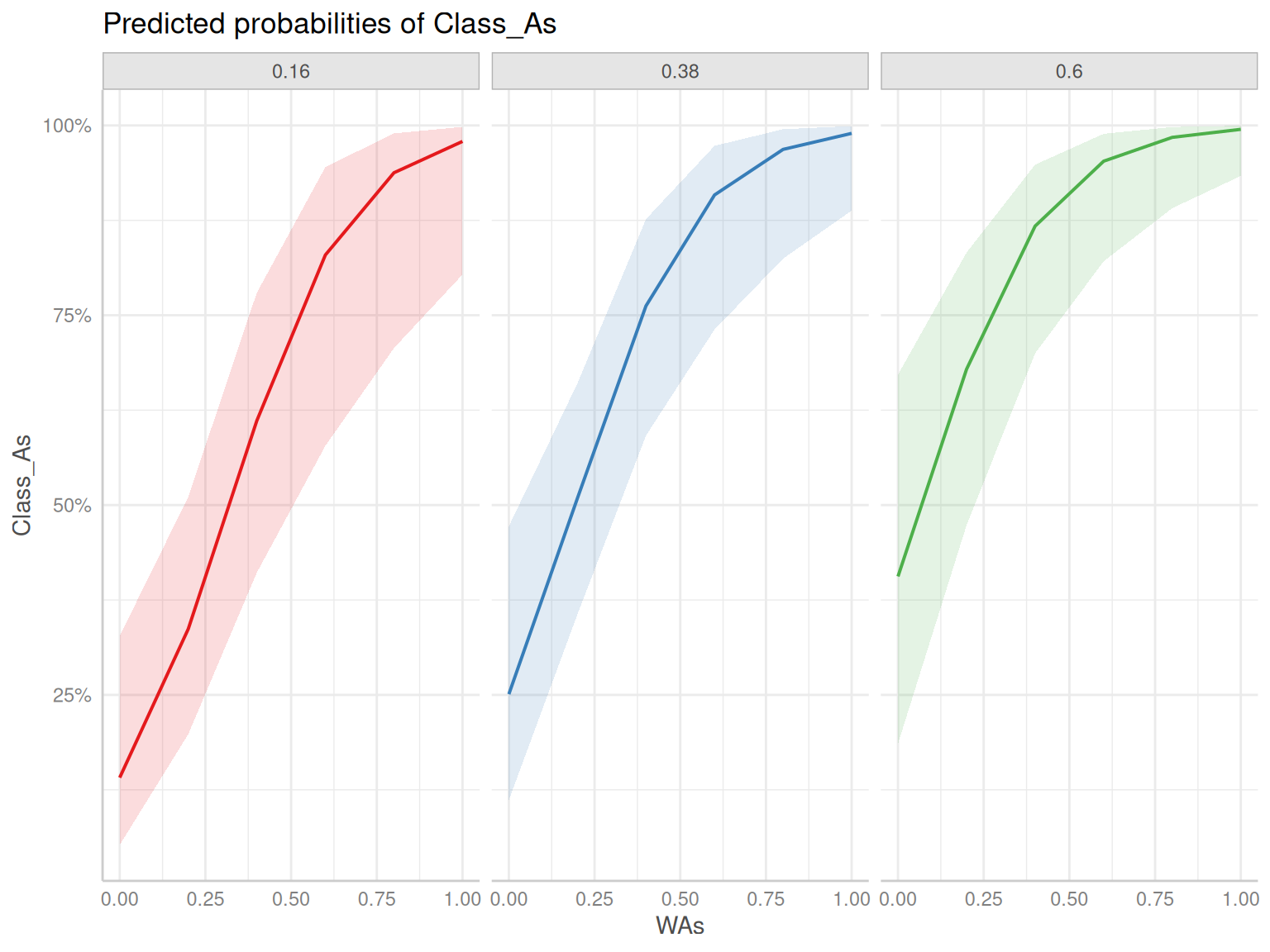
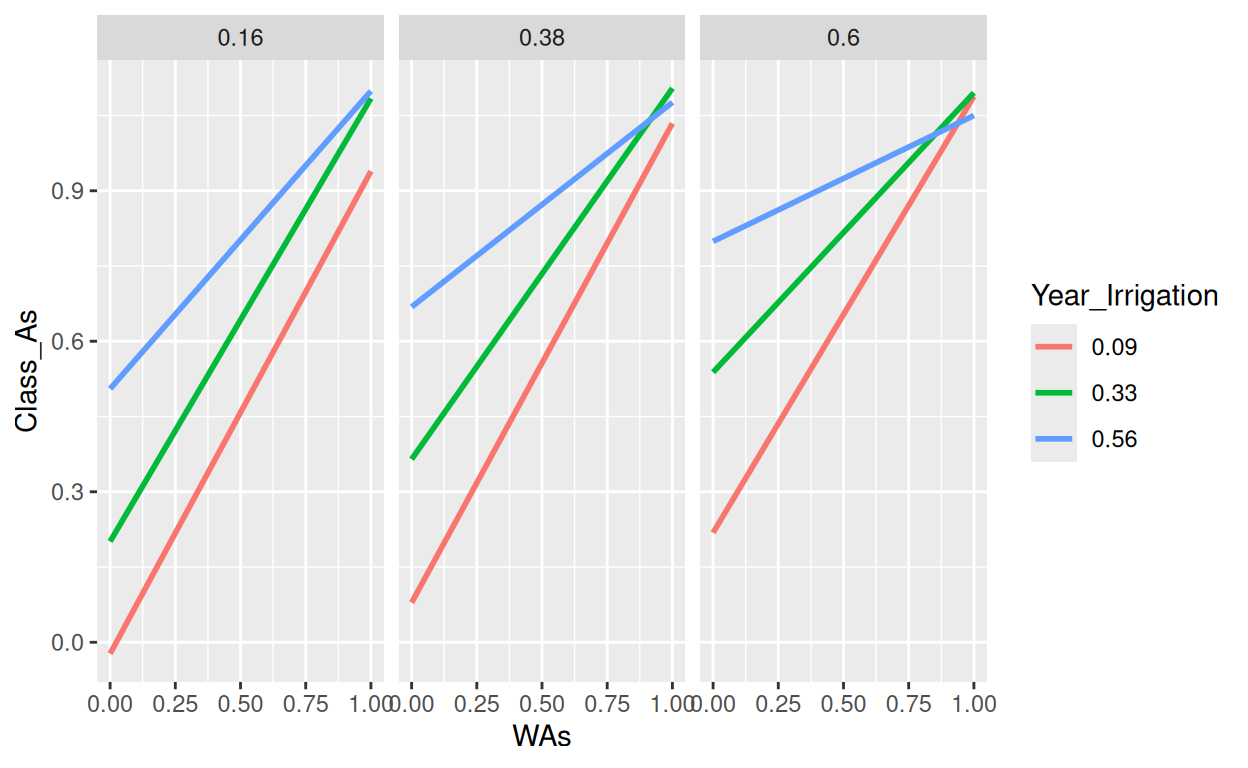
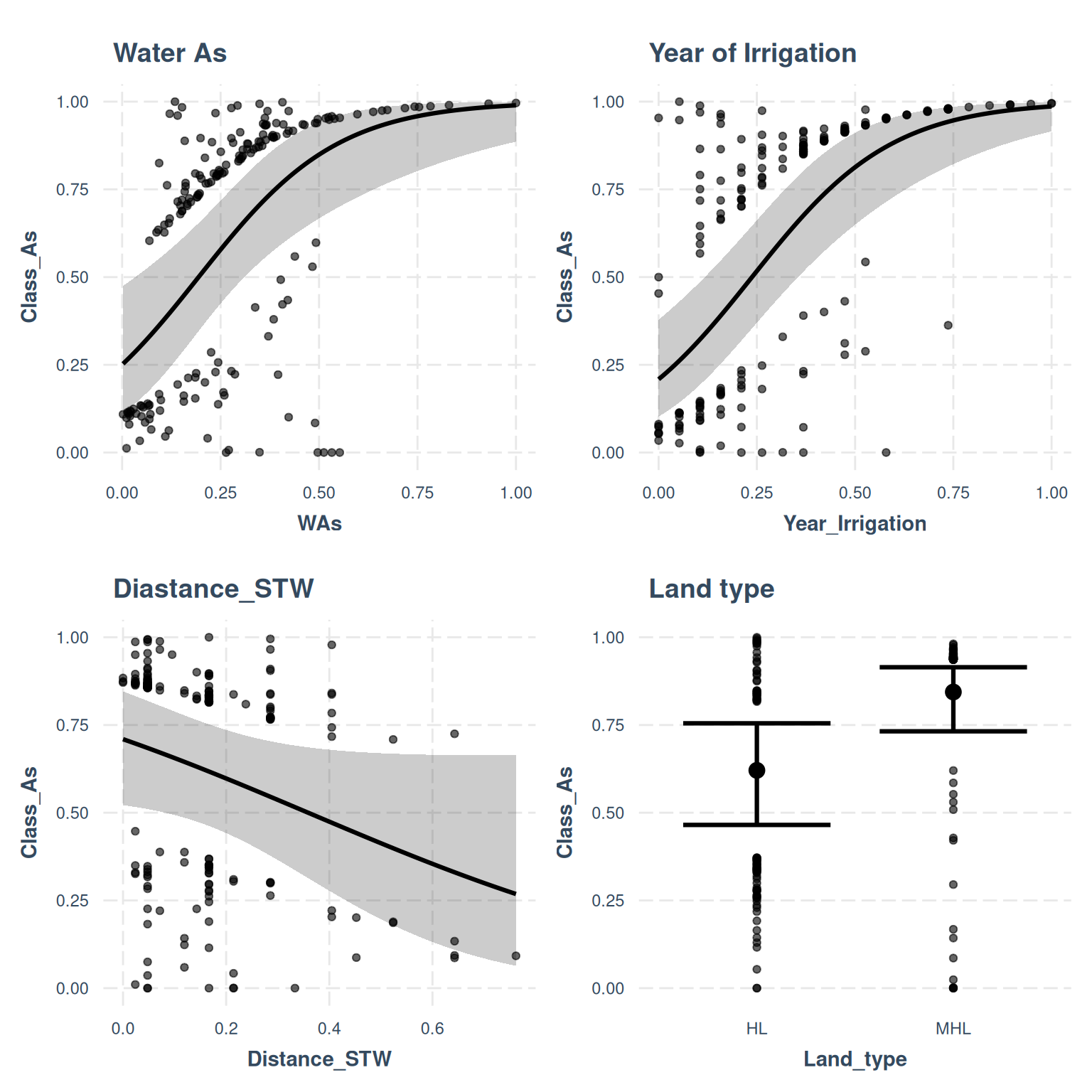
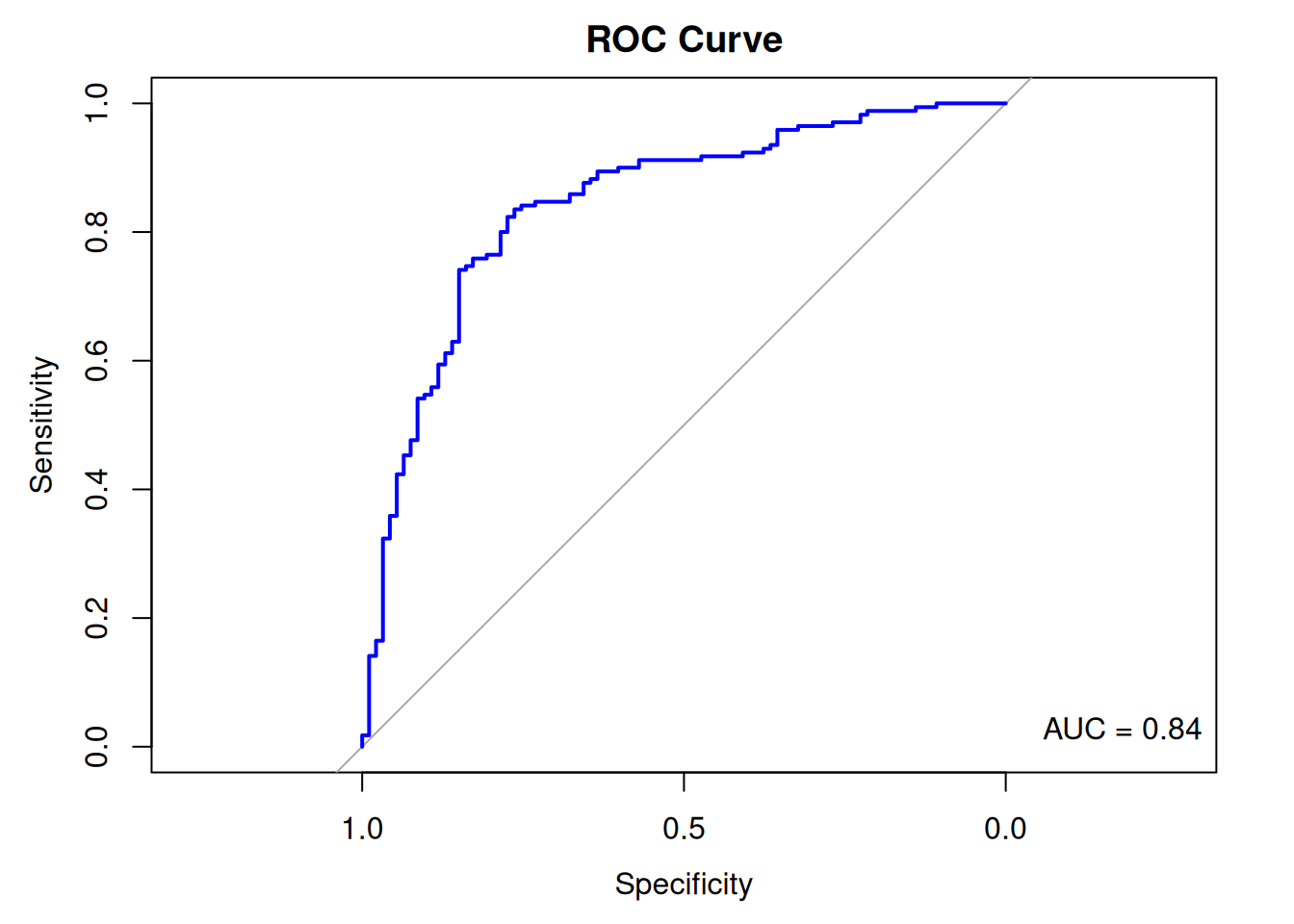
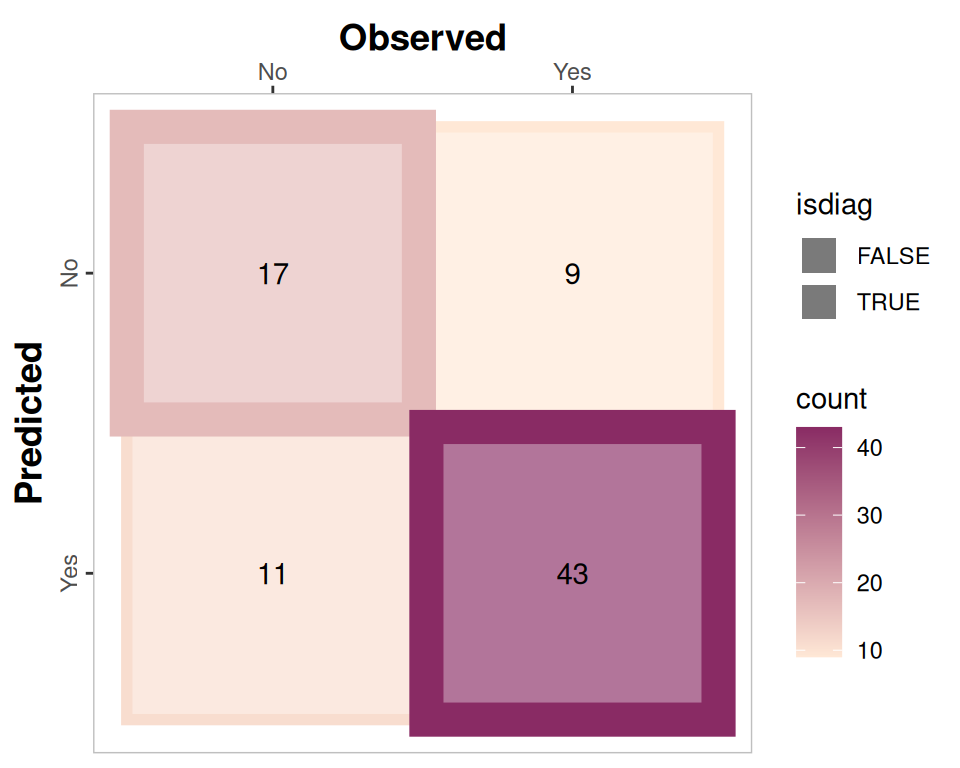
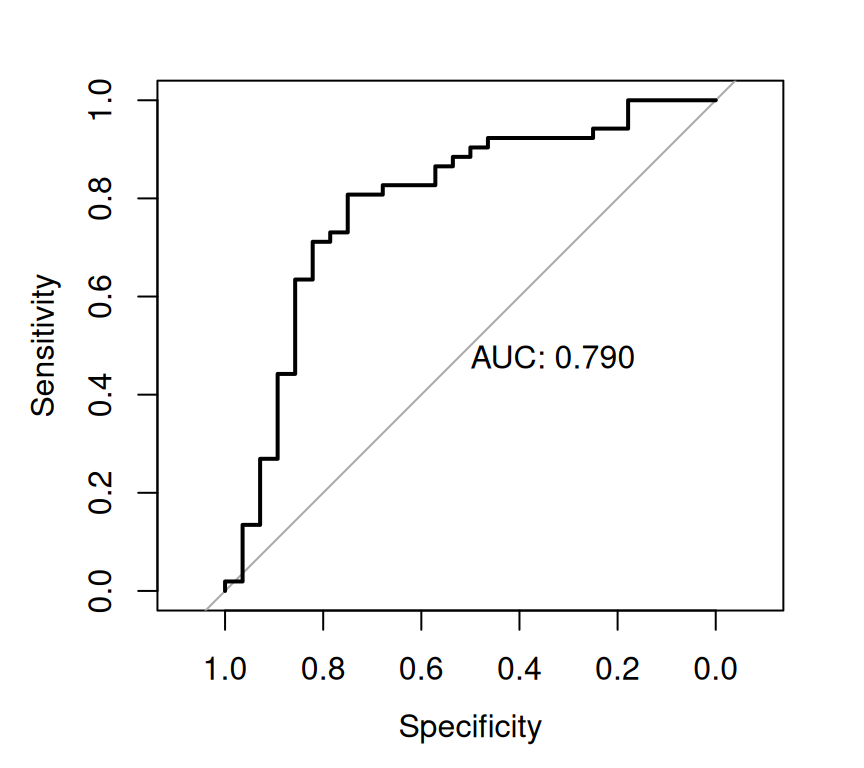
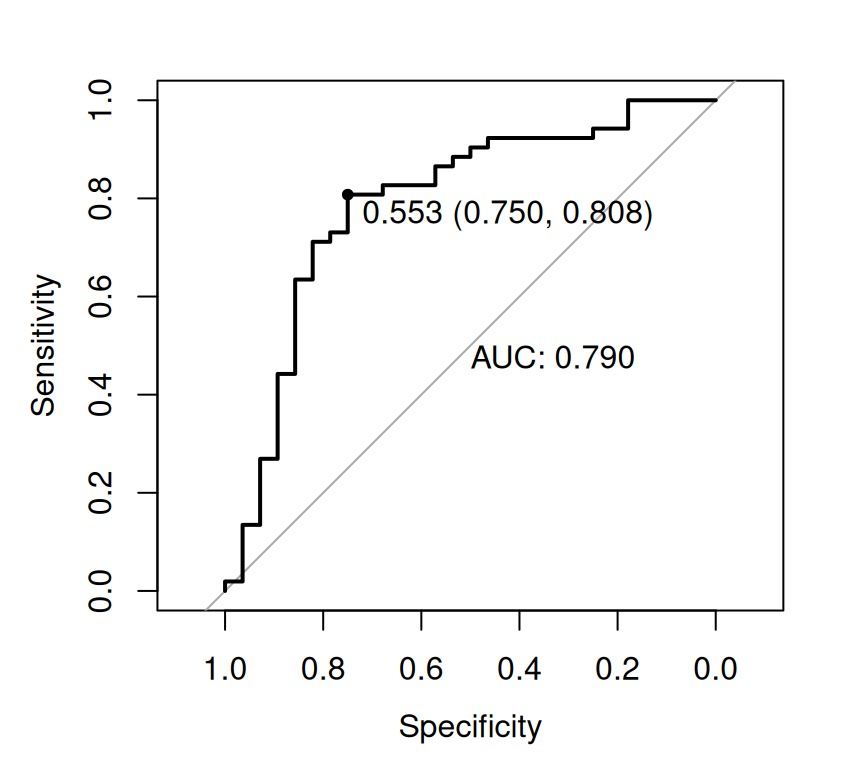
Rows: 263
Columns: 29
$ ID              <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,…
$ Longitude       <dbl> 89.1134, 89.1232, 89.1281, 89.1296, 89.1312, 89.1305, …
$ Latitude        <dbl> 22.7544, 22.7576, 22.7499, 22.7568, 22.7366, 22.7297, …
$ WAs             <dbl> 0.059, 0.059, 0.079, 0.122, 0.072, 0.042, 0.075, 0.064…
$ WP              <dbl> 0.761, 1.194, 1.317, 1.545, 0.966, 1.058, 0.868, 0.890…
$ WFe             <dbl> 3.44, 4.93, 9.70, 8.58, 4.78, 6.95, 7.81, 8.14, 8.99, …
$ WEc             <dbl> 1.03, 1.07, 1.40, 0.83, 1.42, 1.82, 1.71, 1.74, 1.57, …
$ WpH             <dbl> 7.03, 7.06, 6.84, 6.85, 6.95, 6.89, 6.86, 6.98, 6.82, …
$ WMg             <dbl> 33.9, 34.1, 40.5, 28.4, 43.4, 43.2, 50.1, 51.5, 48.2, …
$ WNa             <dbl> 69.4, 74.6, 89.4, 22.8, 93.0, 165.7, 110.5, 127.0, 96.…
$ WCa             <dbl> 99.1, 94.3, 133.9, 103.8, 130.5, 153.3, 172.0, 163.2, …
$ WK              <dbl> 5.3, 5.7, 6.0, 4.0, 5.3, 6.5, 5.9, 6.4, 6.5, 3.7, 4.4,…
$ WS              <dbl> 2.936, 2.826, 2.307, 1.012, 2.511, 2.764, 2.792, 1.562…
$ SAs             <dbl> 29.10, 45.10, 23.20, 23.80, 26.00, 25.60, 26.30, 31.60…
$ SPAs            <dbl> 9.890, 10.700, 5.869, 6.031, 6.627, 9.530, 6.708, 8.63…
$ SAoAs           <dbl> 13.280, 21.900, 12.266, 12.596, 13.805, 13.585, 13.969…
$ SAoFe           <dbl> 2500, 2670, 2160, 2500, 2060, 2500, 2520, 2140, 2150, …
$ SpH             <dbl> 7.74, 7.87, 8.03, 8.07, 7.81, 7.77, 7.66, 7.89, 8.00, …
$ SEc             <dbl> 1.128, 1.021, 1.257, 1.067, 1.354, 1.442, 1.428, 1.385…
$ SOC             <dbl> 1.66, 1.26, 1.36, 1.61, 1.26, 1.74, 1.71, 1.69, 1.41, …
$ SP              <dbl> 13.79, 15.31, 15.54, 16.28, 14.20, 13.41, 13.26, 14.84…
$ Sand            <dbl> 16.3, 11.1, 12.3, 12.7, 12.1, 16.7, 16.8, 13.7, 12.6, …
$ Silt            <dbl> 44.8, 48.7, 46.4, 43.6, 50.9, 43.6, 43.4, 40.8, 44.9, …
$ Clay            <dbl> 38.9, 40.2, 41.3, 43.7, 37.1, 39.8, 39.8, 45.5, 42.4, …
$ Elevation       <dbl> 3, 5, 4, 3, 5, 2, 2, 3, 3, 3, 2, 5, 6, 6, 5, 5, 4, 6, …
$ Year_Irrigation <dbl> 14, 20, 10, 8, 10, 9, 8, 10, 8, 2, 20, 4, 15, 10, 5, 4…
$ Distance_STW    <dbl> 5, 6, 5, 8, 5, 5, 10, 8, 10, 8, 5, 5, 9, 5, 10, 10, 12…
$ Land_type       <chr> "MHL", "MHL", "MHL", "MHL", "MHL", "MHL", "MHL", "MHL"…
$ Land_type_ID    <dbl> 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 1, 1, 1, 1, 1, …

Create a Binary Response Variable

The binary class typically refers to a classification problem where there are only two possible classes or outcomes. As we see SAs is a continuous variable, but we need to convert it into binary class (contaminated and non-contaminated) based on our published paper. The paper suggests that we use the probability of exceeding the upper baseline soil arsenic concentration (14.8 mg/kg) to define soil samples as either As contaminated (Yes) or non-contaminated (No).

Here we will convert Soil As (SAs) into two classes- Yes = Contaminatedand No = noncontaminated and create a new binary response variables (Class_As) with two levels:

Yes = SAs > 14.8 mg As/kg

No = SAs < 14.8 mg As/kg

mf$Class_As<- cut(mf$SAs, 
                   breaks=c(-Inf, 14.8, Inf), 
                   labels=c("No", "Yes"))
mf$Class_As<-as.factor(mf$Class_As)

Box/Violine Plots

We can create a nice looking plots with results of ANOVA and post-hoc tests on the same plot (directly on the boxplots). We will use ggbetweenstats() function of {ggstatsplot} package:

p1<-ggstatsplot::ggbetweenstats(
  data = mf,
  x = Class_As,
  y = WAs,
  ylab = "Water As (ppm)",
  xlab = "As-contamination",
  type = "parametric", # ANOVA or Kruskal-Wallis
  var.equal = TRUE, # ANOVA or Welch ANOVA
  plot.type = "box",
  pairwise.comparisons = TRUE,
  pairwise.display = "significant",
  centrality.plotting = FALSE,
  bf.message = FALSE
)+
# add plot title
ggtitle("Water As") +
   theme(
    # center the plot title
    plot.title = element_text(hjust = 0.5),
    axis.line = element_line(colour = "gray"),
    # axis title font size
    axis.title.x = element_text(size = 14), 
    # X and  axis font size
    axis.text.y=element_text(size=12,vjust = 0.5, hjust=0.5),
    axis.text.x = element_text(size=12))

p2<-ggstatsplot::ggbetweenstats(
  data = mf,
  x = Class_As,
  y = WFe,
  ylab = "Water Fe (%)",
  xlab = "As-contamination",
  type = "parametric", # ANOVA or Kruskal-Wallis
  var.equal = TRUE, # ANOVA or Welch ANOVA
  plot.type = "box",
  pairwise.comparisons = TRUE,
  pairwise.display = "significant",
  centrality.plotting = FALSE,
  bf.message = FALSE
)+
# add plot title
ggtitle("   Water Fe") +
   theme(
    # center the plot title
    plot.title = element_text(hjust = 0.5),
    axis.line = element_line(colour = "gray"),
    # axis title font size
    axis.title.x = element_text(size = 14), 
    # X and  axis font size
    axis.text.y=element_text(size=12,vjust = 0.5, hjust=0.5),
    axis.text.x = element_text(size=12))

p3<-ggstatsplot::ggbetweenstats(
  data = mf,
  x = Class_As,
  y = SAoFe,
  ylab = "Soil Oxlate-Fe",
  xlab = "As-contamination",
  type = "parametric", # ANOVA or Kruskal-Wallis
  var.equal = TRUE, # ANOVA or Welch ANOVA
  plot.type = "box",
  pairwise.comparisons = TRUE,
  pairwise.display = "significant",
  centrality.plotting = FALSE,
  bf.message = FALSE
)+
# add plot title
ggtitle("Soil Oxalate Extractable Fe") +
   theme(
    # center the plot title
    plot.title = element_text(hjust = 0.5),
    axis.line = element_line(colour = "gray"),
    # axis title font size
    axis.title.x = element_text(size = 14), 
    # X and  axis font size
    axis.text.y=element_text(size=12,vjust = 0.5, hjust=0.5),
    axis.text.x = element_text(size=12))

p4<-ggstatsplot::ggbetweenstats(
  data = mf,
  x = Class_As,
  y = SOC,
  ylab = "Soil OC (%)",
  xlab = "As-contamination",
  type = "parametric", # ANOVA or Kruskal-Wallis
  var.equal = TRUE, # ANOVA or Welch ANOVA
  plot.type = "box",
  pairwise.comparisons = TRUE,
  pairwise.display = "significant",
  centrality.plotting = FALSE,
  bf.message = FALSE
)+
# add plot title
ggtitle("Soil Organic Carbon") +
   theme(
    # center the plot title
    plot.title = element_text(hjust = 0.5),
    axis.line = element_line(colour = "gray"),
    # axis title font size
    axis.title.x = element_text(size = 14), 
    # X and  axis font size
    axis.text.y=element_text(size=12,vjust = 0.5, hjust=0.5),
    axis.text.x = element_text(size=12))

(p1|p2)/(p3|p4)

Data Processing

df <- mf |> 
  # select variables
  dplyr::select (WAs,  WFe,  
                SAoFe, SOC, 
                Year_Irrigation, Distance_STW,
                Land_type, Class_As) |> 
   # convert to factor
   dplyr::mutate_at(vars(Land_type), funs(factor))  |> 
   dplyr::mutate_at(vars(Class_As), funs(factor))  |> 
   # normalize the all numerical features 
   dplyr::mutate_at(1:6,  funs((.-min(.))/max(.-min(.)))) |> 
   glimpse()

Rows: 263
Columns: 8
$ WAs             <dbl> 0.10738255, 0.10738255, 0.15212528, 0.24832215, 0.1364…
$ WFe             <dbl> 0.1804348, 0.3423913, 0.8608696, 0.7391304, 0.3260870,…
$ SAoFe           <dbl> 0.3807107, 0.4238579, 0.2944162, 0.3807107, 0.2690355,…
$ SOC             <dbl> 0.5333333, 0.3428571, 0.3904762, 0.5095238, 0.3428571,…
$ Year_Irrigation <dbl> 0.68421053, 1.00000000, 0.47368421, 0.36842105, 0.4736…
$ Distance_STW    <dbl> 0.04761905, 0.07142857, 0.04761905, 0.11904762, 0.0476…
$ Land_type       <fct> MHL, MHL, MHL, MHL, MHL, MHL, MHL, MHL, MHL, MHL, MHL,…
$ Class_As        <fct> Yes, Yes, Yes, Yes, Yes, Yes, Yes, Yes, Yes, No, Yes, …

Split Data

seeds = 11076
tr_prop = 0.70
# training data (70% data)
train= plyr::ddply(df,.(Land_type, Class_As),
                 function(., seed) { set.seed(seed); .[sample(1:nrow(.), trunc(nrow(.) * tr_prop)), ] }, seed = 101)
test = plyr::ddply(df, .(Land_type, Class_As),
            function(., seed) { set.seed(seed); .[-sample(1:nrow(.), trunc(nrow(.) * tr_prop)), ] }, seed = 101)

print(prop.table(table(train$Class_As)))

       No       Yes 
0.3551913 0.6448087 

print(prop.table(table(test$Class_As)))

  No  Yes 
0.35 0.65 

Fit a Logistic Model

We will use logistic regression to predict probability of soil As contamination (Class_As) based on elevation, year of irrigation, distance from STW, several irrigation water, and soil properties. We will use glm() function with family = binomial(link = "logit")) for logistic regression. The Class_As variable will be used as a response variable, while all the other variables in the train will serve as predictors.

fit.logit<-glm(Class_As~., data= train,
             family = binomial(link = "logit"))

Model Summary

summary(fit.logit)

Call:
glm(formula = Class_As ~ ., family = binomial(link = "logit"), 
    data = train)

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)      -4.6213     1.1250  -4.108 3.99e-05 ***
WAs               5.6470     1.6189   3.488 0.000486 ***
WFe               3.2410     1.1112   2.917 0.003538 ** 
SAoFe             1.1407     1.3045   0.874 0.381870    
SOC               1.0756     1.7309   0.621 0.534310    
Year_Irrigation   5.6052     1.2039   4.656 3.23e-06 ***
Distance_STW     -2.4892     1.3771  -1.808 0.070668 .  
Land_typeMHL      1.1958     0.4563   2.621 0.008779 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 238.12  on 182  degrees of freedom
Residual deviance: 142.73  on 175  degrees of freedom
AIC: 158.73

Number of Fisher Scoring iterations: 6

The summary output of GLM has several components that provide valuable insights into the model’s performance. The summary includes information on the call, residuals, and coefficients, which are analogous to the summary of a model fit using the lm() function. However, the GLM summary differs from the lm() function in providing additional information about the dispersion parameter and deviance values.

The intercept represents the log-odds of the event happening when all independent variables are set to zero. In some cases, interpreting the intercept might not be meaningful, especially if setting all variables to zero is not a realistic or meaningful scenario in your context.

Each slope coefficient represents the change in the log-odds of the event happening for a one-unit change in the corresponding independent variable holding all other variables constant. If the slope is positive, an increase in the corresponding independent variable is associated with an increase in the log-odds of the event happening. If the slope is negative, an increase in the corresponding independent variable is associated with a decrease in the log-odds of the event happening.

The dispersion parameter is a scaling factor that accounts for the variance of the response variable and is a crucial component of the GLM models. The deviance values are measures of the model’s goodness of fit and are used to assess how well the model fits the observed data.

In cases where quasi-family is not used, the dispersion value is set to 1. This value indicates that the model’s variance equals the mean and performs adequately. By understanding the summary output of a GLM model, we can make informed decisions about the model’s performance and take the necessary steps to improve its accuracy.

summ() function of {jtools} produce summary table of regression models:

jtools::summ(fit.logit)

Observations	183
Dependent variable	Class_As
Type	Generalized linear model
Family	binomial
Link	logit

𝛘²(7)	95.39
p	0.00
Pseudo-R² (Cragg-Uhler)	0.56
Pseudo-R² (McFadden)	0.40
AIC	158.73
BIC	184.41

	Est.	S.E.	z val.	p
(Intercept)	-4.62	1.12	-4.11	0.00
WAs	5.65	1.62	3.49	0.00
WFe	3.24	1.11	2.92	0.00
SAoFe	1.14	1.30	0.87	0.38
SOC	1.08	1.73	0.62	0.53
Year_Irrigation	5.61	1.20	4.66	0.00
Distance_STW	-2.49	1.38	-1.81	0.07
Land_typeMHL	1.20	0.46	2.62	0.01
Standard errors: MLE

Interpretation of Logistic Model

We can use reoprt() function of {report} package to further explain the fit.glm object.

report(fit.logit)

We fitted a logistic model (estimated using ML) to predict Class_As with WAs,
WFe, SAoFe, SOC, Year_Irrigation, Distance_STW and Land_type (formula: Class_As
~ WAs + WFe + SAoFe + SOC + Year_Irrigation + Distance_STW + Land_type). The
model's explanatory power is substantial (Tjur's R2 = 0.46). The model's
intercept, corresponding to WAs = 0, WFe = 0, SAoFe = 0, SOC = 0,
Year_Irrigation = 0, Distance_STW = 0 and Land_type = HL, is at -4.62 (95% CI
[-6.99, -2.56], p < .001). Within this model:

  - The effect of WAs is statistically significant and positive (beta = 5.65, 95%
CI [2.66, 9.03], p < .001; Std. beta = 1.06, 95% CI [0.50, 1.69])
  - The effect of WFe is statistically significant and positive (beta = 3.24, 95%
CI [1.17, 5.55], p = 0.004; Std. beta = 0.71, 95% CI [0.26, 1.22])
  - The effect of SAoFe is statistically non-significant and positive (beta =
1.14, 95% CI [-1.40, 3.75], p = 0.382; Std. beta = 0.19, 95% CI [-0.23, 0.62])
  - The effect of SOC is statistically non-significant and positive (beta = 1.08,
95% CI [-2.29, 4.52], p = 0.534; Std. beta = 0.16, 95% CI [-0.35, 0.69])
  - The effect of Year Irrigation is statistically significant and positive (beta
= 5.61, 95% CI [3.40, 8.15], p < .001; Std. beta = 1.32, 95% CI [0.80, 1.91])
  - The effect of Distance STW is statistically non-significant and negative
(beta = -2.49, 95% CI [-5.32, 0.15], p = 0.071; Std. beta = -0.36, 95% CI
[-0.77, 0.02])
  - The effect of Land type [MHL] is statistically significant and positive (beta
= 1.20, 95% CI [0.31, 2.11], p = 0.009; Std. beta = 1.20, 95% CI [0.31, 2.11])

Standardized parameters were obtained by fitting the model on a standardized
version of the dataset. 95% Confidence Intervals (CIs) and p-values were
computed using a Wald z-distribution approximation.

Model Performance

performance::performance(fit.logit)

# Indices of model performance

AIC     |    AICc |     BIC | Tjur's R2 |  RMSE | Sigma | Log_loss | Score_log
------------------------------------------------------------------------------
158.731 | 159.559 | 184.407 |     0.456 | 0.354 | 1.000 |    0.390 |      -Inf

AIC     | Score_spherical |   PCP
---------------------------------
158.731 |           0.011 | 0.751

Note

Tjur's R², also known as Tjur’s coefficient of discrimination, is a measure of discrimination or predictive accuracy for binary outcomes in logistic regression. It assesses how well the model distinguishes between the two categories of the dependent variable. Tjur’s R² is defined as the difference in the average predicted probabilities of the two outcomes.

The formula for Tjur’s R² is as follows:

\[ R^2_{Tjur} = P(Y=1|\hat{Y}=1) - P(Y=0|\hat{Y}=1) \]

Here:

• \(P(Y=1|\hat{Y}=1)\) is the probability of the actual outcome being 1 given that the predicted outcome is 1.

• \(P(Y=0|\hat{Y}=1)\) is the probability of the actual outcome being 0 given that the predicted outcome is 1.

Tjur’s R² ranges from -1 to 1, where a higher value indicates better discrimination. A positive value suggests that the model is better at predicting the positive class, while a negative value suggests better prediction for the negative class.

In practice, Tjur’s R² is not as commonly used as other metrics like the area under the ROC curve (AUC) or the Brier score, but it provides a measure of the practical significance of the logistic regression model in terms of discrimination. Keep in mind that the interpretation of Tjur’s R² should be done in the context of the specific dataset and problem you are working on.

Log_loss: Logarithmic Loss (Log Loss), also known as cross-entropy loss, is a commonly utilized loss function in machine learning, particularly in classification problems. It measures the performance of a classification model that outputs a probability value ranging from 0 to 1. Due to its versatility and capability to handle prediction errors, Logarithmic Loss is often preferred over alternative loss functions. Its formulation is mathematically rigorous, and its implementation is straightforward, making it an essential tool for any machine learning practitioner.

The formula for Log Loss is:

\[ {Log Loss} = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(p_i) + (1 - y_i) \log(1 - p_i)] \]

Where:

• \(N\) is the number of samples in the dataset.

• \(y_i\) is the true label for the \(i\) th sample (0 or 1 for binary classification, or one-hot encoded vectors for multiclass classification).

• \(p_i\) is the predicted probability that the \(i\) th sample belongs to the positive class.

Score_spherical: A proper scoring rule is a mathematical function used to assess the accuracy of probabilistic predictions made by a model. It is called proper because it is designed to maximize the expected score when the model’s predictions align with the actual probabilities of the outcomes.

PCP: Percentage of Correct Predictions (PCP), also known as accuracy, is a common evaluation metric for models with binary outcomes. It measures the proportion of correctly predicted instances out of the total number of instances.

Visualization of model assumptions

The package {performance} provides many functions to check model assumptions, like check_collinearity(), check_normality() or check_heteroscedasticity(). To get a comprehensive check, use check_model()

performance::check_model(fit.logit)

The Logistic Distribution of Intercept and Slopes

The plogis() function is used to calculate the logistic cumulative distribution function (CDF) of Intercept and Slopes. The logistic CDF is the probability that a logistic random variable is less than or equal to a specified value. The plogis() function takes a numeric vector of values and returns the corresponding probabilities.

The plogis() function is particularly useful in the context of logistic regression, where you might be interested in converting log-odds into probabilities. If you have a logistic regression model with coefficients (intercept and slopes), you can use the logistic function and plogis to calculate probabilities.

## Intercept
intercept = coef(fit.logit)[1]
# Back-transform the  Slope of WAs
slop_was = coef(fit.logit)[2]
log_odds<-intercept + (slop_was*train$WAs)
probabilities <- plogis(log_odds)
age.prob<-data.frame(WAs = train$WAs, LogOdds = log_odds, Probability = probabilities) |>   
  glimpse()

Rows: 183
Columns: 3
$ WAs         <dbl> 0.01789709, 0.07158837, 0.05816555, 0.25727069, 0.01789709…
$ LogOdds     <dbl> -4.520209, -4.217012, -4.292812, -3.168459, -4.520209, -4.…
$ Probability <dbl> 0.01076951, 0.01452844, 0.01348219, 0.04037006, 0.01076951…

Odds Ratio (OR)

# Calculate odds ratios
odds_ratios <- exp(coef(fit.logit))
print(odds_ratios)

    (Intercept)             WAs             WFe           SAoFe             SOC 
   9.840252e-03    2.834474e+02    2.555898e+01    3.128973e+00    2.931829e+00 
Year_Irrigation    Distance_STW    Land_typeMHL 
   2.718239e+02    8.297822e-02    3.306285e+00 

The tbl_regression() function from the {gtsummary} package takes a regression model object as input and produces a formatted table with Odd-ratio and confidence interval.

tbl_regression(fit.logit,  exp = TRUE)

Characteristic	OR	95% CI	p-value
WAs	283	14.3, 8,389	<0.001
WFe	25.6	3.21, 257	0.004
SAoFe	3.13	0.25, 42.6	0.4
SOC	2.93	0.10, 91.9	0.5
Year_Irrigation	272	30.0, 3,470	<0.001
Distance_STW	0.08	0.00, 1.17	0.071
Land_type
HL	—	—
MHL	3.31	1.36, 8.25	0.009
Abbreviations: CI = Confidence Interval, OR = Odds Ratio

The tab_model() function of {sjPlot} package also creates HTML tables from regression models:

tab_model(fit.logit)

	Class_As
Predictors	Odds Ratios	CI	p
(Intercept)	0.01	0.00 – 0.08	<0.001
WAs	283.45	14.30 – 8389.46	<0.001
WFe	25.56	3.21 – 257.00	0.004
SAoFe	3.13	0.25 – 42.61	0.382
SOC	2.93	0.10 – 91.93	0.534
Year Irrigation	271.82	30.04 – 3470.06	<0.001
Distance STW	0.08	0.00 – 1.17	0.071
Land type [MHL]	3.31	1.36 – 8.25	0.009
Observations	183
R2 Tjur	0.456

plot_model() function of {sjPlot} package creates plots the estimates from logistic model:

plot_model(fit.logit, vline.color = "red")

Marginal Effects and Adjusted Predictions

The presentation of regression models, typically in the form of tables, is widely accepted as a clear and accessible method for interpreting results. However, for more intricate models that incorporate interaction or transformed terms, such as quadratic or spline terms, the use of raw regression coefficients may prove less effective, resulting in challenges when interpreting outcomes. In such cases, adjusted predictions or marginal means provide a more fitting solution. The use of visual aids can also assist in the comprehension of such effects or predictions, providing an intuitive understanding of the relationship between predictors and outcomes, even for complex models.

If we want the marginal effects for “WAs”, you may use margins() function of {margins} package:

margins::margins(fit.logit, variables = "WAs")

    WAs
 0.7018

we get the same marginal effect using avg_slopes() function from the {marginaleffects} package

marginaleffects::avg_slopes(fit.logit, variables = "WAs")

 Estimate Std. Error    z Pr(>|z|)    S 2.5 % 97.5 %
    0.702      0.177 3.96   <0.001 13.7 0.355   1.05

Term: WAs
Type:  response 
Comparison: dY/dX

To calculate marginal effects and adjusted predictions, the predict_response() function is used. This function can return three types of predictions, namely, conditional effects, marginal effects or marginal means, and average marginal effects or counterfactual predictions. You can set the type of prediction you want by using the emperical argument.

effect<-ggeffects::predict_response(fit.logit, "WAs", margin = "empirical")

Data were 'prettified'. Consider using `terms="WAs [all]"` to get smooth
  plots.

effect

# Average predicted probabilities of Class_As

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.39 | 0.21, 0.61
0.20 |      0.66 | 0.55, 0.76
0.40 |      0.86 | 0.75, 0.92
0.60 |      0.95 | 0.85, 0.98
0.80 |      0.98 | 0.90, 1.00
1.00 |      0.99 | 0.94, 1.00

The marginal effects of “MHL”, relative to “HL” is:

effect$predicted[2] - effect$predicted[1]

[1] 0.2743284

was.wfe <- predict_response(fit.logit, terms = c("WAs", "WFe"))
plot(was.wfe, facets = TRUE)

was.year.wfe<- predict_response(fit.logit, terms = c("WAs", "Year_Irrigation", "WFe"))
was.year.wfe

# Predicted probabilities of Class_As

Year_Irrigation: 0.09
WFe: 0.16

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.04 | 0.01, 0.14
0.20 |      0.12 | 0.05, 0.25
0.60 |      0.56 | 0.27, 0.82
1.00 |      0.93 | 0.54, 0.99

Year_Irrigation: 0.09
WFe: 0.38

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.08 | 0.03, 0.22
0.20 |      0.22 | 0.12, 0.37
0.60 |      0.73 | 0.44, 0.90
1.00 |      0.96 | 0.70, 1.00

Year_Irrigation: 0.09
WFe: 0.6

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.15 | 0.05, 0.38
0.20 |      0.36 | 0.19, 0.58
0.60 |      0.84 | 0.58, 0.96
1.00 |      0.98 | 0.81, 1.00

Year_Irrigation: 0.33
WFe: 0.16

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.14 | 0.05, 0.33
0.20 |      0.34 | 0.20, 0.52
0.60 |      0.83 | 0.58, 0.95
1.00 |      0.98 | 0.81, 1.00

Year_Irrigation: 0.33
WFe: 0.38

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.26 | 0.11, 0.48
0.20 |      0.52 | 0.36, 0.67
0.60 |      0.91 | 0.74, 0.97
1.00 |      0.99 | 0.89, 1.00

Year_Irrigation: 0.33
WFe: 0.6

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.41 | 0.19, 0.68
0.20 |      0.68 | 0.48, 0.84
0.60 |      0.95 | 0.82, 0.99
1.00 |      0.99 | 0.93, 1.00

Year_Irrigation: 0.56
WFe: 0.16

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.38 | 0.16, 0.66
0.20 |      0.65 | 0.43, 0.83
0.60 |      0.95 | 0.80, 0.99
1.00 |      0.99 | 0.93, 1.00

Year_Irrigation: 0.56
WFe: 0.38

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.55 | 0.29, 0.79
0.20 |      0.79 | 0.61, 0.91
0.60 |      0.97 | 0.88, 0.99
1.00 |      1.00 | 0.96, 1.00

Year_Irrigation: 0.56
WFe: 0.6

 WAs | Predicted |     95% CI
-----------------------------
0.00 |      0.72 | 0.42, 0.90
0.20 |      0.89 | 0.72, 0.96
0.60 |      0.99 | 0.93, 1.00
1.00 |      1.00 | 0.98, 1.00

Adjusted for:
*        SAoFe = 0.40
*          SOC = 0.39
* Distance_STW = 0.16
*    Land_type =   HL

# select specific levels for grouping terms
ggplot(was.year.wfe, aes(x = x, y = predicted, colour = group)) +
  stat_smooth(method = "lm", se = FALSE) +
  facet_wrap(~facet) +
  labs(
    y = get_y_title(was.year.wfe),
    x = get_x_title(was.year.wfe),
    colour = get_legend_title(was.year.wfe)
  )

effect_plot() function of {jtools} package plot simple effects in a logistic regression model:

p1<-jtools::effect_plot(fit.logit, 
                    main.title = "Water As", 
                    pred = WAs, 
                    interval = TRUE,  
                    partial.residuals = TRUE)
p2<-jtools::effect_plot(fit.logit, 
                    main.title = "Year of Irrigation ", 
                    pred = Year_Irrigation, 
                    interval = TRUE,  
                    partial.residuals = TRUE)
p3<-jtools::effect_plot(fit.logit, 
                    main.title = "Diastance_STW", 
                    pred = Distance_STW , 
                    interval = TRUE,  
                    partial.residuals = TRUE)
p4<-jtools::effect_plot(fit.logit,
                    main.title = "Land type", 
                    pred = Land_type, 
                    interval = TRUE,  
                    partial.residuals = TRUE)
library(patchwork)
(p1+p2)/(p3 +p4)

Cross-validation

k-fold Cross-validation

The {boot} package’s cv.glm() function provides an easy way to do k-fold cross-validation on GLM models. Here first we fit GLM model for entire dataset then we apply cv.glm() on fitted glm object.

## Define cost function (for misclassification error)
cost <- function(r, pi) {
  # Convert predicted probabilities to binary predictions
  predictions <- ifelse(pi > 0.5, 1, 0)
  # Calculate the misclassification error
  mean(predictions != r)
}

fit.logit.mf<-glm(Class_As~., data= mf,
             family = binomial(link = "logit"))
cv_result <- cv.glm(data = mf, glmfit = fit.logit.mf, K = 5, cost = cost)

# Print cross-validation error
print(cv_result$delta)

[1] 0.04942966 0.03956975

However, this cv.glm() function does not directly provide predicted classes for each observation in the test folds; it only provides the cross-validated error estimates. However, we can achieve this by manually implementing k-fold cross-validation and storing the predictions for each fold.

# Custom cross-validation function to get predicted classes
cross_validation_glm_predictions <- function(formula, data, k = 5, family = binomial, seed = 123) {
  set.seed(seed)
  
  n <- nrow(data)
  folds <- sample(rep(1:k, length.out = n))
  
  # Initialize a vector to store predicted probabilities
  all_probabilities <- numeric(n)
  
  for (i in 1:k) {
    train_data <- data[folds != i, ]
    test_data <- data[folds == i, ]
    
    # Fit GLM model
    model <- glm(formula = formula, data = train_data, family = family)
    
    # Predict probabilities for the test set
    test_probabilities <- predict(model, newdata = test_data, type = "response")
    
    # Store probabilities in the correct positions
    all_probabilities[folds == i] <- test_probabilities
  }
  
  return(all_probabilities)
}

# cress-validation
predicted_prob <- cross_validation_glm_predictions(
  formula = Class_As ~ WAs + WFe +  SAoFe + SOC + Year_Irrigation + Distance_STW + Land_type,
  data = mf,
  k = 5,
  family = binomial
)

Cross-validation Performance

## predicted class
predicted_classes<-ifelse(predicted_prob  > 0.5, 1 ,0)
# actual class
actual_classes<-ifelse(mf$Class_As=="Yes", 1, 0)
# Calculate True Positives, False Positives, True Negatives, False Negatives
TP <- sum(actual_classes == 1 & predicted_classes == 1)
FP <- sum(actual_classes == 0 & predicted_classes == 1)
TN <- sum(actual_classes == 0 & predicted_classes == 0)
FN <- sum(actual_classes == 1 & predicted_classes == 0)

# Calculate Accuracy
accuracy <- (TP + TN) / (TP + FP + TN + FN)

# Calculate Precision
precision <- TP / (TP + FP)

# Calculate Recall
recall <- TP / (TP + FN)

# Calculate F1 Score
f1_score <- 2 * (precision * recall) / (precision + recall)

# Display results
cat("Accuracy:", accuracy, "\n")

Accuracy: 0.7984791 

cat("Precision:", precision, "\n")

Precision: 0.8232044 

cat("Recall:", recall, "\n")

Recall: 0.8764706 

cat("F1 Score:", f1_score, "\n")

F1 Score: 0.8490028 

ROC Curve

The ROC analysis can easily be performed using roc() function of {pROC} package.

  #| warning: false
#| error: false
#| fig.width: 4.5
#| fig.height: 4

# compute ROC
roc_curve <- roc(actual_classes, predicted_prob )

Setting levels: control = 0, case = 1

Setting direction: controls < cases

# Plot the ROC curve
plot(roc_curve, main = "ROC Curve", col = "blue", lwd = 2)

# Add AUC to the plot
auc_value <- auc(roc_curve)
legend("bottomright", legend = paste("AUC =", round(auc_value, 2)), bty = "n")

Prediction at Test Locations

Prediction

The predict() function for logistic models returns the default predictions of log-odds, which are probabilities on the logit scale. When type = response, the function provides the predicted probabilities.

test$Pred_prob<-predict(fit.logit, test, type = "response")
# setting the cut-off probability
test$Pred_Class<- ifelse(test$Pred_prob > 0.5,"Yes","No")

Confusion Matrix at 50% Cut-Off

# Confusion matrix, proportion of cases
confusion_matrix = table(Actual = test$Class_As, Predicted =test$Pred_Class) 
confusion_matrix

      Predicted
Actual No Yes
   No  17  11
   Yes  9  43

confusion_matrix() function of {metrica} package creates a confusion matrix table or plot displaying the agreement between the observed and the predicted classes by the model.

test |> confusion_matrix(obs = Class_As, pred = Pred_Class, 
                                      plot = TRUE,
                                      colors = c(low="#ffe8d6" , high="#892b64"), 
                                      unit = "count")

Prediction Performance

# define variables
    TP <- confusion_matrix[2, 2]
    TN <- confusion_matrix[1, 1]
    FP <- confusion_matrix[2, 1]
    FN <- confusion_matrix[1, 2]

    # accuracy
    accuracy <- (TP + TN) / sum(confusion_matrix)

    # precision 
    precision <- TP / (TP + FP)

    # Recall 
    recall <- TP / (TP + FN)

    # specificity 
    specificity <- TN / (TN + FP)

    # f1_score 
    f1_score <- 2 * (precision * recall) / (precision + recall)

    # Print the results
    cat("Accuracy:", accuracy, "\n")

Accuracy: 0.75 

    cat("Precision:", precision, "\n")

Precision: 0.8269231 

    cat("Recall:", recall, "\n")

Recall: 0.7962963 

    cat("Specificity:", specificity, "\n")

Specificity: 0.6538462 

    cat("F1 Score:", f1_score, "\n")

F1 Score: 0.8113208 

metrics_summary() function of {metrica} package estimates a group of metrics characterizing the prediction performance of the model:

# Get a selected list at once with metrics_summary()
selected_class_metrics <- c("accuracy", "precision", "recall", "Specificity",  "fscore")

# Binary
test %>% 
  metrics_summary(data = ., 
                  obs = Class_As, pred = Pred_Class, 
                  type = "classification",
                  metrics_list = selected_class_metrics, pos_level = 1) 

     Metric     Score
1  accuracy 0.7500000
2 precision 0.6538462
3    recall 0.6071429
4    fscore 0.6296296

ROC Curve

The ROC analysis can easily be performed using roc() function of {pROC} package.

# Compute roc
library(pROC)
res.roc <- pROC::roc(test$Class_As, test$Pred_prob)
plot.roc(res.roc, print.auc = TRUE)

On a graph, the gray diagonal line represents a classifier’s performance that is no better than random chance. In contrast, a high-performing classifier will exhibit a ROC curve that rises steeply towards the top-left corner. This indicates that it can correctly identify a large number of positives without misclassifying many negatives. The AUC metric is commonly used to evaluate the performance of a classifier. An AUC value close to 1, which is the maximum possible value, is indicative of a highly effective classifier. In this case, our classifier exhibits an AUC value of 0.79, suggesting that it is indeed good. By contrast, a classifier that performs no better than random chance would have an AUC value of 0.5 when assessed using an independent test set that was not used for training the model.

# Extract some interesting results
roc.data <-tibble(
  thresholds = res.roc$thresholds,
  sensitivity = res.roc$sensitivities,
  specificity = res.roc$specificities
)
# Get the probability threshold for specificity = 0.5
roc.data  |> 
  filter(specificity >= 0.5)

# A tibble: 62 × 3
   thresholds sensitivity specificity
        <dbl>       <dbl>       <dbl>
 1      0.333       0.904       0.5  
 2      0.364       0.885       0.5  
 3      0.374       0.885       0.536
 4      0.391       0.865       0.536
 5      0.405       0.865       0.571
 6      0.416       0.846       0.571
 7      0.437       0.827       0.571
 8      0.478       0.827       0.607
 9      0.513       0.827       0.643
10      0.524       0.827       0.679
# ℹ 52 more rows

plot.roc(res.roc, print.auc = TRUE, print.thres = "best")

Summary and Conclusion

This tutorial provided a comprehensive guide to logistic regression in R, focusing on model building, interpretation, and evaluation. It began by constructing a logistic regression model from scratch, which helped us understand the fundamental calculations involved in the process. We then used the glm() function, a convenient and widely-used function in R, to fit a logistic model, demonstrating a more practical application of logistic regression to real datasets. Next, we explored model interpretation, highlighting how to extract and understand coefficients from the glm() output. Specifically, the coefficients represent changes in log odds, and transforming them into odds ratios facilitates easier interpretation. This way, we can see the effect size of each predictor on the outcome. The tutorial emphasized the importance of assessing performance through cross-validation and a hold-out test data set for model evaluation. Cross-validation was employed to estimate the model’s predictive accuracy by repeatedly splitting the data into training and validation sets. This helped us evaluate how the model performs on unseen data.

A hold-out test set also provided an unbiased estimate of model performance, ensuring we avoided overfitting the training data. Logistic regression is a powerful and interpretable tool for binary classification problems, and R’s glm() function allows for its efficient implementation. Through our hands-on approach, we gained insights into the model’s mechanics by building it from scratch and learned to trust our results through robust evaluation techniques. Understanding model interpretation through log-odds and odds ratios reveals each predictor’s influence, making logistic regression especially valuable in fields that require transparent and interpretable models. important factors influencing binary outcomes, and gain insights into the relationships between predictors and outcome probabilities.

References

1. How to Perform Logistic Regression in R

2. Evaluation of Classification Model Accuracy: Essentials

3. Precision, Recall and F1-Score using R

4. Chapter 6 Binary Logistic Regression

5. Chapter 10 Binary Logistic Regression

6. R Online Manual: glm

7. Applied Logistic Regression (Second Edition) by David Hosmer and Stanley Lemeshow)

8. Stat Books for Loan, Logistic Regression and Limited Dependent Variables

Session Info

sessionInfo()