4. Aalen’s Additive Regression Model

This section provides an overview of the Aalen’s Additive regression model in survival analysis, including its key concepts, applications, and how to fit the model manually in R. We will also demonstrate how to fit the Aalen model using the aareg() function from the {survival} package and the aalen() function from the {timereg} package in R.

Overview

The Aalen’s Additive regression model, also known as the Aalen’s additive hazards model, is a statistical technique used in survival analysis. Unlike the more commonly used Cox Proportional Hazards model, which assumes a multiplicative relationship between the covariates and the hazard function, the Aalen model assumes an additive relationship between the covariates and the hazard function. This model is particularly useful when the proportional hazards assumption of the Cox model does not hold, meaning that the effects of covariates on survival are not constant over time.

Key Concepts of the Aalen Model:

  1. Additive Hazards:
    • In the Aalen model, the hazard at time \(t\) is expressed as the sum of contributions from the covariates. The contribution of each covariate to the hazard function can change over time, making the model more flexible than the Cox model.
    • The hazard function \(h(t)\)is expressed as an additive function of the covariates.
  2. Time-Varying Coefficients:
    • The Aalen model allows for time-varying effects of the covariates, meaning that the effect of each covariate on the hazard can change over time. This is an important feature that differentiates it from other survival models like the Cox model, which assumes constant covariate effects.
  3. No Proportional Hazards Assumption:
    • The model does not rely on the proportional hazards assumption, making it more appropriate for situations where the covariates’ effects vary over time.
  4. Interpretation:
    • The coefficients in the Aalen model represent the incremental effects of the covariates on the hazard function at each time point. These coefficients are not hazard ratios, as in the Cox model, but are rather additive effects.

The Aalen additive hazards model can be written as:

\[ h(t|X) = h_0(t) + \beta_1(t) X_1 + \beta_2(t) X_2 + \dots + \beta_p(t) X_p \]

Where:

  • \(h(t|X)\) is the hazard at time \(t\) for an individual with covariates \(X_1, X_2, \dots, X_p\).
  • \(h_0(t)\) is the baseline hazard function at time \(t\).
  • \(\beta_1(t), \beta_2(t), \dots, \beta_p(t)\) are the time-varying coefficients for each covariate \(X_1, X_2, \dots, X_p\), indicating how the effect of each covariate on the hazard changes over time.

Key Differences Between the Aalen Model and Cox Model:

  1. Additive vs. Multiplicative:
    • Aalen model: Assumes an additive effect of covariates on the hazard function.
    • Cox model: Assumes a multiplicative effect of covariates on the hazard function.
  2. Time-Varying Coefficients:
    • Aalen model: Allows for time-varying effects of covariates (i.e., the effect of a covariate can change over time).
    • Cox model: Assumes the effects of covariates (hazard ratios) are constant over time.
  3. Proportional Hazards Assumption:
    • Aalen model: Does not require the proportional hazards assumption.
    • Cox model: Requires the proportional hazards assumption (the effect of covariates on the hazard is proportional over time).
  4. Interpretation:
    • Aalen model: Coefficients represent additive contributions to the hazard rate, which vary over time.
    • Cox model: Coefficients represent multiplicative hazard ratios, which are assumed to be constant over time.

Applications of the Aalen Model:

  1. Time-Varying Effects:
    • The Aalen model is particularly useful when the effects of covariates are expected to change over time. For example, in medical research, the effect of a treatment may change as patients progress through different stages of their disease.
  2. Exploratory Analysis:
    • It is often used for exploratory analysis to check whether the proportional hazards assumption holds. If the covariate effects appear to be time-varying in the Aalen model, it suggests that the Cox model may not be appropriate.
  3. Flexible Survival Modeling:
    • The model provides more flexibility than the Cox model, especially when the effects of covariates are not constant over time.

Advantages of the Aalen Model:

  1. Flexibility:
    • The model allows for time-varying covariate effects, making it useful when the proportional hazards assumption does not hold.
  2. Exploratory Tool:
    • It can be used to explore time-varying effects of covariates and identify whether a simpler Cox model is appropriate.
  3. No Proportional Hazards Assumption:
    • It does not require the proportional hazards assumption, making it more robust in certain settings.

Limitations:

  1. Interpretability:
    • The coefficients are harder to interpret compared to hazard ratios in the Cox model, especially because they are time-varying and represent additive effects.
  2. Less Popular:
    • The Aalen model is less commonly used than the Cox model, which means there is less software support and fewer resources available for interpreting results.
  3. Less Efficient:
    • If the true underlying model is multiplicative (as assumed by the Cox model), the Aalen model may be less efficient in estimating the effects of covariates.

Aalen Model Scratch

Let’s now go through the manual calculation of Aalen’s Additive Hazard Model using the simulated veteran dataset. We’ll calculate the necessary steps for fitting the model without relying on any pre-built R package functions.

We will:

  1. Simulate the veteran-like dataset.
  2. Estimate the time-varying coefficients.
  3. Calculate the cumulative coefficients.
  4. Compute the cumulative hazard.
  5. Plot the cumulative coefficients.

Create a dataset

Here we simulate a dataset with variables similar to those in the veteran dataset.

Code 
set.seed(123)

# Number of patients
n <- 100

# Simulated dataset similar to 'veteran'
simulated_veteran <- data.frame(
  time = rexp(n, rate = 0.1),  # Survival times from an exponential distribution
  status = sample(0:1, n, replace = TRUE, prob = c(0.4, 0.6)),  # Event (1) or censoring (0)
  trt = sample(1:2, n, replace = TRUE),  # Treatment group (1 = standard, 2 = test)
  age = rnorm(n, mean = 60, sd = 10),  # Age (mean = 60)
  celltype = sample(1:4, n, replace = TRUE),  # Cell type (categorical: 1 = squamous, etc.)
  karno = rnorm(n, mean = 70, sd = 10),  # Karnofsky score
  diagtime = rnorm(n, mean = 5, sd = 2),  # Time since diagnosis in months
  prior = sample(0:10, n, replace = TRUE)  # Number of prior therapies
)

head(simulated_veteran)
        time status trt      age celltype    karno  diagtime prior
1  8.4345726      0   1 71.09920        4 56.35963 6.4254067     7
2  5.7661027      0   2 60.84737        1 67.99219 7.1695502     0
3 13.2905487      0   1 67.54054        1 78.65779 0.5500246     1
4  0.3157736      0   2 55.00708        4 68.98117 7.4713869    10
5  0.5621098      1   1 62.14445        3 76.24187 2.5179110     4
6  3.1650122      1   1 56.75314        4 79.59005 5.9095385     4

This generates 100 observations with the following columns: - time: Survival or censoring time. - status: Event indicator (1 = event occurred, 0 = censored). - trt: Treatment group (1 or 2). - age, karno, diagtime, and prior: Covariates for analysis.

Estimate Time-Varying Coefficients

At each event time, we estimate the time-varying coefficients ( _j(t) ) using least squares regression. The formula for the coefficient estimates is:

\[ \beta(t) = \left( X(t)^T X(t) \right)^{-1} X(t)^T d(t) \] Here’s the code to estimate the coefficients manually at each event time:

Code 
# Load MASS package
library(MASS)

estimate_aalen_coefficients <- function(time, status, X) {
  unique_times <- sort(unique(time[status == 1]))  # Only event times
  betas <- matrix(0, nrow = length(unique_times), ncol = ncol(X))  # To store coefficients
  
  for (i in seq_along(unique_times)) {
    t <- unique_times[i]
    
    # Risk set at time t (those who haven't had the event yet)
    risk_set <- which(time >= t)
    
    if (length(risk_set) > 1) {
      X_risk <- X[risk_set, , drop = FALSE]
      y_risk <- status[risk_set]
      
      # Use Moore-Penrose generalized inverse
      betas[i, ] <- ginv(t(X_risk) %*% X_risk) %*% t(X_risk) %*% y_risk
    }
  }
  
  return(list(betas = betas, unique_times = unique_times))
}

# Prepare the design matrix X (excluding the time and status columns)
X <- as.matrix(simulated_veteran[, c("trt", "age", "karno", "diagtime", "prior")])

# Try running it again with generalized inverse
aalen_results <- estimate_aalen_coefficients(simulated_veteran$time, simulated_veteran$status, X)

# Extract the results
betas <- aalen_results$betas
unique_times <- aalen_results$unique_times

# Convert to a data frame for easier plotting
betas_df <- as.data.frame(betas)
betas_df$time <- unique_times

# Print the estimated time-varying coefficients
head(betas_df)
          V1          V2          V3          V4         V5      time
1 0.05873544 0.006259231 0.003374983 -0.02853867 0.01010860 0.2915345
2 0.06448842 0.005070569 0.003717400 -0.02450852 0.01455075 0.3176774
3 0.05570305 0.005388397 0.003540725 -0.02264181 0.01307701 0.4208829
4 0.04973973 0.005907833 0.003585505 -0.02391420 0.00942069 0.5621098
5 0.05503656 0.005802184 0.003284665 -0.02139353 0.01007015 0.6737589
6 0.04506262 0.005664981 0.003475025 -0.01908471 0.01108399 0.9863089

Calculate Cumulative Coefficients

After obtaining the time-varying coefficients at each event time, we calculate the cumulative coefficients by summing them over time:

\[ \hat{\beta_j}(t) = \sum_{t_i \leq t} \hat{\beta_j}(t_i) \]

Code 
# Calculate cumulative coefficients
cumulative_betas <- apply(betas, 2, cumsum)

# Convert to a data frame for easier plotting
cumulative_betas_df <- as.data.frame(cumulative_betas)
cumulative_betas_df$time <- unique_times

# Print the cumulative coefficients
head(cumulative_betas_df)
          V1          V2          V3          V4         V5      time
1 0.05873544 0.006259231 0.003374983 -0.02853867 0.01010860 0.2915345
2 0.12322386 0.011329800 0.007092383 -0.05304719 0.02465934 0.3176774
3 0.17892691 0.016718197 0.010633109 -0.07568900 0.03773635 0.4208829
4 0.22866664 0.022626031 0.014218614 -0.09960320 0.04715704 0.5621098
5 0.28370320 0.028428214 0.017503279 -0.12099673 0.05722719 0.6737589
6 0.32876583 0.034093196 0.020978304 -0.14008144 0.06831118 0.9863089

Compute the Cumulative Hazard

The cumulative hazard is the integral (sum) of the hazard function over time, where the hazard function at any time is the sum of the covariates weighted by their time-varying coefficients:

\[ \Lambda(t \mid X) = \sum_{t_i \leq t} h(t_i \mid X) \]

For simplicity, we’ll assume that we only calculate this for the baseline hazard.

Plot Cumulative Coefficients

Finally, we plot the cumulative coefficients for each covariate to see how their effects change over time.

Code 
# Plot cumulative coefficients for each covariate
plot(cumulative_betas_df$time, cumulative_betas_df$V1, type = "l", col = "blue",
     xlab = "Time", ylab = "Cumulative Coefficient", lwd = 2, main = "Cumulative Coefficients of Aalen's Additive Model")
lines(cumulative_betas_df$time, cumulative_betas_df$V2, col = "red", lwd = 2)
lines(cumulative_betas_df$time, cumulative_betas_df$V3, col = "green", lwd = 2)
lines(cumulative_betas_df$time, cumulative_betas_df$V4, col = "purple", lwd = 2)
lines(cumulative_betas_df$time, cumulative_betas_df$V5, col = "orange", lwd = 2)

# Add a legend
legend("topright", legend = c("Treatment", "Age", "Karnofsky", "Diagnosis Time", "Prior Therapies"),
       col = c("blue", "red", "green", "purple", "orange"), lwd = 2)

Aalen Model in R

This tutorial is mostly used two R packages {survival}, and {timereg}.

Install Required R Packages

Following R packages are required to run this notebook. If any of these packages are not installed, you can install them using the code below:

Code 
packages <-c(
         'tidyverse',
         'report',
         'performance',
         'gtsummary',
         'MASS',
         'epiDisplay',
         'survival',
         'survminer',
         'ggsurvfit',
         'tidycmprsk',
         'ggfortify',
         'timereg',
         'cmprsk',
         'condSURV',
         'riskRegression'
         )
#| warning: false
#| error: false

# Install missing packages
new_packages <- packages[!(packages %in% installed.packages()[,"Package"])]
if(length(new_packages)) install.packages(new_packages)
 
devtools::install_github("ItziarI/WeDiBaDis")

# Verify installation
cat("Installed packages:\n")
print(sapply(packages, requireNamespace, quietly = TRUE))

Load Packages

Code 
# Load packages with suppressed messages
invisible(lapply(packages, function(pkg) {
  suppressPackageStartupMessages(library(pkg, character.only = TRUE))
}))
Code 
# Check loaded packages
cat("Successfully loaded packages:\n")
Successfully loaded packages:
Code 
print(search()[grepl("package:", search())])
 [1] "package:riskRegression" "package:condSURV"       "package:cmprsk"        
 [4] "package:timereg"        "package:ggfortify"      "package:tidycmprsk"    
 [7] "package:ggsurvfit"      "package:survminer"      "package:ggpubr"        
[10] "package:epiDisplay"     "package:nnet"           "package:survival"      
[13] "package:foreign"        "package:gtsummary"      "package:performance"   
[16] "package:report"         "package:lubridate"      "package:forcats"       
[19] "package:stringr"        "package:dplyr"          "package:purrr"         
[22] "package:readr"          "package:tidyr"          "package:tibble"        
[25] "package:ggplot2"        "package:tidyverse"      "package:MASS"          
[28] "package:stats"          "package:graphics"       "package:grDevices"     
[31] "package:utils"          "package:datasets"       "package:methods"       
[34] "package:base"

Data

In this example, we will perform a Aalen additive hazards model using the veteran dataset from the {survival} package.

Code 
data(veteran)
Warning in data(veteran): data set 'veteran' not found
Code 
glimpse(veteran)
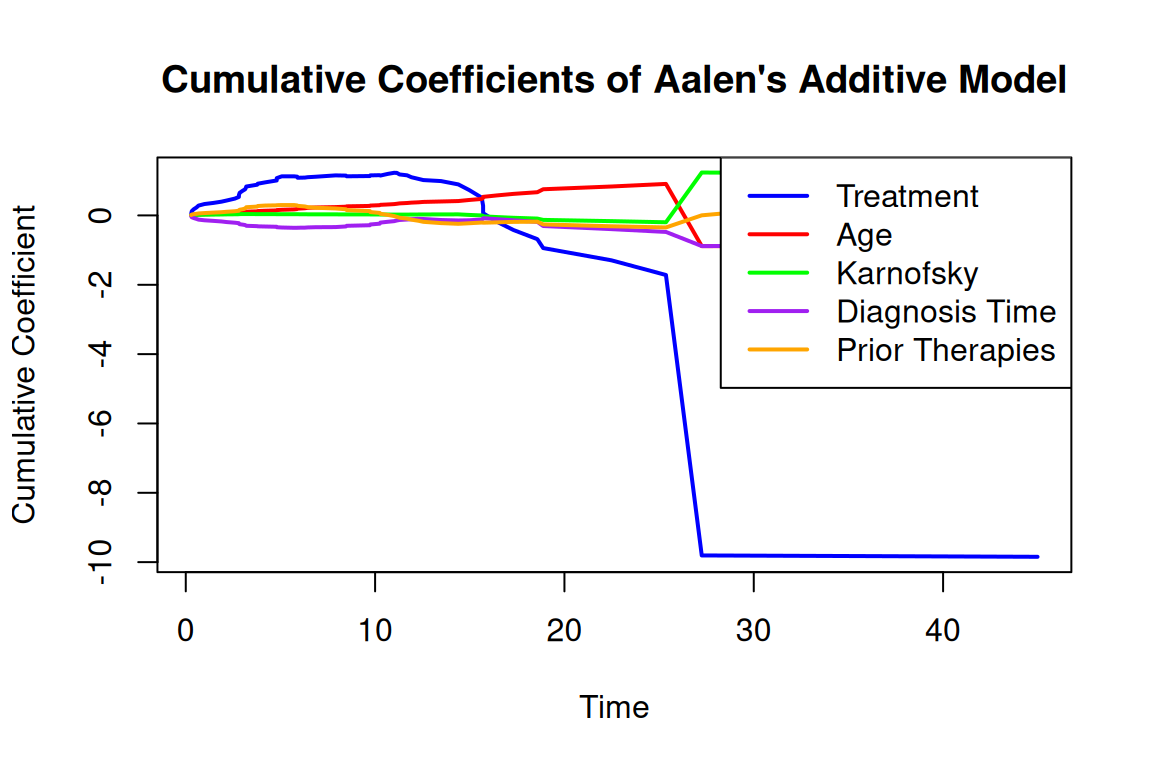
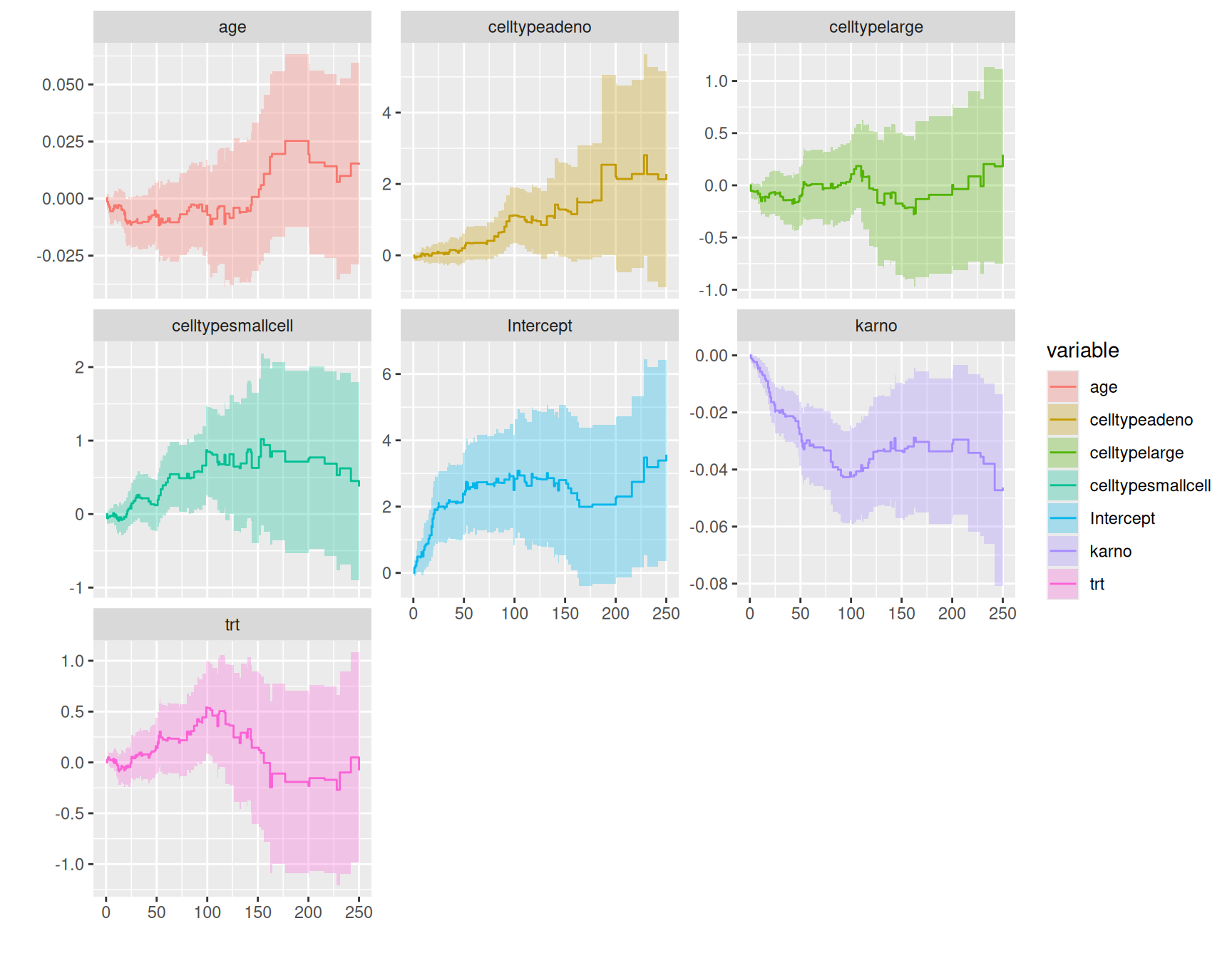
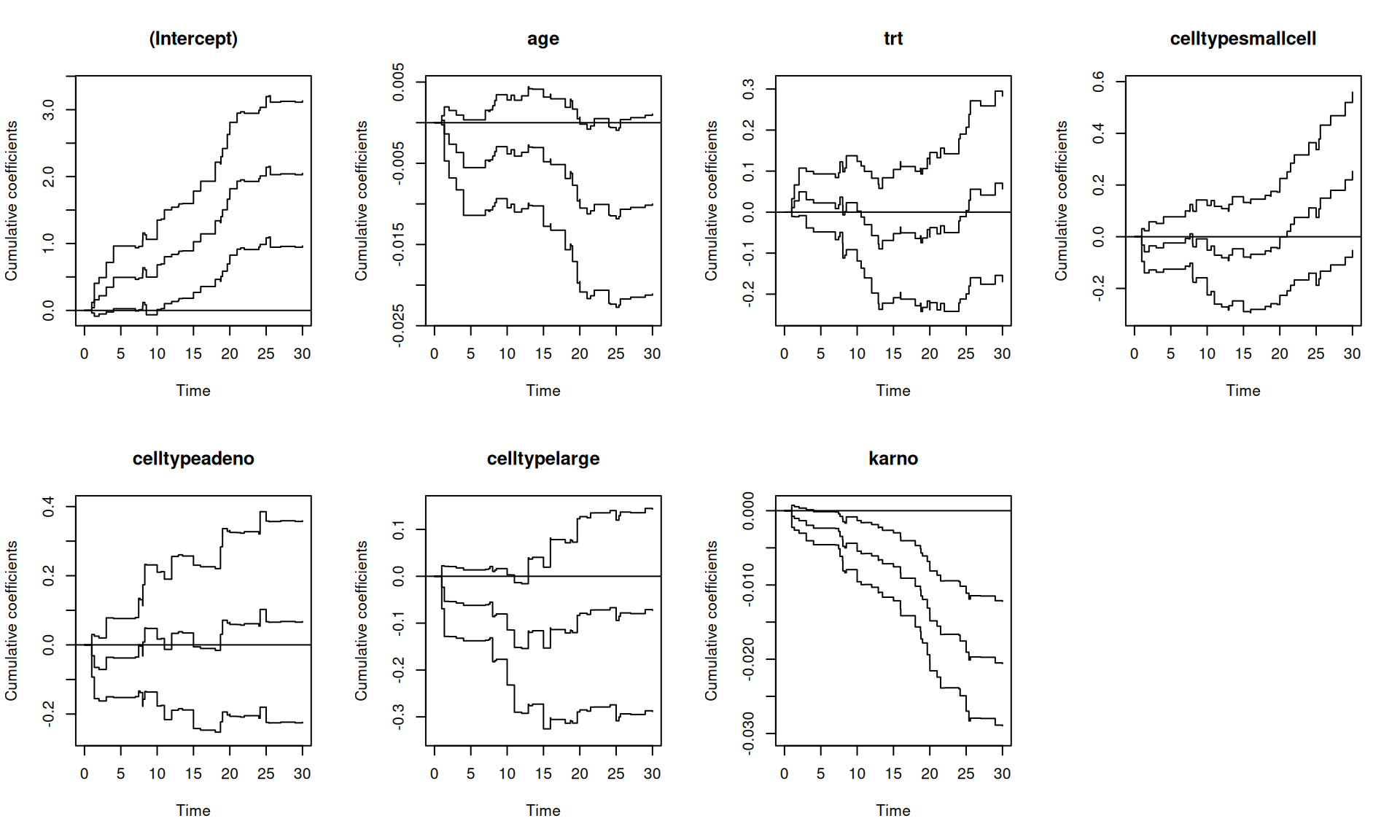
Rows: 137
Columns: 8
$ trt      <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ celltype <fct> squamous, squamous, squamous, squamous, squamous, squamous, s…
$ time     <dbl> 72, 411, 228, 126, 118, 10, 82, 110, 314, 100, 42, 8, 144, 25…
$ status   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0…
$ karno    <dbl> 60, 70, 60, 60, 70, 20, 40, 80, 50, 70, 60, 40, 30, 80, 70, 6…
$ diagtime <dbl> 7, 5, 3, 9, 11, 5, 10, 29, 18, 6, 4, 58, 4, 9, 11, 3, 9, 2, 4…
$ age      <dbl> 69, 64, 38, 63, 65, 49, 69, 68, 43, 70, 81, 63, 63, 52, 48, 6…
$ prior    <dbl> 0, 10, 0, 10, 10, 0, 10, 0, 0, 0, 0, 10, 0, 10, 10, 0, 0, 0, …

The dataset contains information such as:

  • time: Survival time in days.

  • status: Censoring indicator (1 = death, 0 = censored).

  • trt: Treatment group (1 = standard treatment, 2 = test treatment).

  • age: Age of the patient.

  • celltype: Cell type of lung cancer.

  • karno: Karnofsky performance score (higher is better).

  • diagtime: Time since diagnosis in months.

  • prior: Number of prior treatments.

Fit a Aalen Model using {survival} package

aareg() function of {survival} package using the survival time (time), censoring indicator (status), and several covariates such as age, trt, celltype, and karno,

Code 
fit.aamodel <-aareg(Surv(time, status) ~  age + trt + celltype + karno , 
                 data = veteran)
summary(fit.aamodel)
                      slope      coef se(coef)      z        p
Intercept          0.067600  3.74e-02 1.06e-02  3.540 4.00e-04
age               -0.000249 -6.86e-05 1.28e-04 -0.537 5.91e-01
trt                0.006840  2.54e-03 2.62e-03  0.971 3.32e-01
celltypesmallcell  0.015100  6.64e-03 3.40e-03  1.950 5.07e-02
celltypeadeno      0.023500  1.04e-02 4.18e-03  2.490 1.27e-02
celltypelarge     -0.000918  3.87e-04 2.85e-03  0.136 8.92e-01
karno             -0.001250 -4.54e-04 8.81e-05 -5.160 2.52e-07

Chisq=40.27 on 6 df, p=4.02e-07; test weights=aalen

The summary of the model shows the time-varying estimates for each covariate (e.g., age, treatment, cell type, and Karnofsky score).

  • If the estimates for a covariate remain roughly constant over time, it suggests that its effect on the hazard is constant.

  • If the estimates for a covariate change over time, it indicates that the covariate has a time-varying effect on survival.

Code 
aareg(Surv(time, status) ~  age + trt + celltype + karno , 
                 data = veteran) |>  
  tbl_regression(exp = TRUE)
Characteristic exp(Beta) 95% CI p-value
Intercept 1.04 1.02, 1.06 <0.001
age 1.00 1.00, 1.00 0.6
trt 1.00 1.00, 1.01 0.3
celltypesmallcell 1.01 1.00, 1.01 0.051
celltypeadeno 1.01 1.00, 1.02 0.013
celltypelarge 1.00 1.0, 1.01 0.9
karno 1.00 1.00, 1.00 <0.001
Abbreviation: CI = Confidence Interval

We can visualize how the cumulative regression coefficients (i.e., the effect of each covariate) change over time by plotting the model.

Code 
autoplot(fit.aamodel)

The plot shows how the cumulative effect of each covariate on the hazard function changes over time. This allows us to see whether the covariate effects are constant or time-varying.

  • Age: If the cumulative coefficient for age increases over time, it suggests that older patients have a progressively higher risk of death as time goes on.

  • Treatment (trt): The plot for trt will show how the effect of the treatment group changes over time. If the test treatment has a decreasing or flat cumulative coefficient, it suggests a positive effect on survival.

  • Karnofsky score (karno): If the cumulative coefficient for karno decreases, it suggests that patients with a higher Karnofsky score (better performance status) have a reduced risk of death.

Fit a Aalen Model using {timereg} package

aalen() function of {timereg} package fits both the additive hazards model of Aalen and the semi-parametric additive hazards model of McKeague and Sasieni. Estimates are un-weighted. Time dependent variables and counting process data (multiple events per subject) are possible.

max.time: end of observation period where estimates are computed. Estimates thus computed from [start.time, max.time]. Default is max of data.

n.sim: number of simulations in resampling.

Code 
# Fit the Aalen additive hazards model
fit.aalenreg <- aalen(Surv(time, status) ~ age + trt + celltype + karno, 
                      data = veteran,
                      max.time=30, # 
                      n.sim=1000)

# Print the summary of the model
summary(fit.aalenreg)
Additive Aalen Model 

Test for nonparametric terms 

Test for non-significant effects 
                  Supremum-test of significance p-value H_0: B(t)=0
(Intercept)                                4.41               0.000
age                                        2.26               0.166
trt                                        1.76               0.448
celltypesmallcell                          1.66               0.436
celltypeadeno                              1.60               0.447
celltypelarge                              2.22               0.145
karno                                      5.37               0.000

Test for time invariant effects 
                        Kolmogorov-Smirnov test p-value H_0:constant effect
(Intercept)                             0.49900                       0.207
age                                     0.00421                       0.450
trt                                     0.11400                       0.167
celltypesmallcell                       0.21700                       0.018
celltypeadeno                           0.07560                       0.806
celltypelarge                           0.12500                       0.064
karno                                   0.00274                       0.586
                          Cramer von Mises test p-value H_0:constant effect
(Intercept)                            1.23e+00                       0.351
age                                    1.34e-04                       0.350
trt                                    1.04e-01                       0.128
celltypesmallcell                      5.36e-01                       0.006
celltypeadeno                          3.28e-02                       0.805
celltypelarge                          1.16e-01                       0.056
karno                                  8.44e-05                       0.295

   
   
  Call: 
aalen(formula = Surv(time, status) ~ age + trt + celltype + karno, 
    data = veteran, max.time = 30, n.sim = 1000)

To visualize how the effect of each covariate changes over time, you can plot the cumulative regression coefficients.

Code 
par(mfrow=c(2,4))
plot(fit.aalenreg)

Interpretation of the Results

  • Karnofsky Score (karno): A negative time-varying coefficient indicates that better performance status (higher Karnofsky score) is associated with a lower hazard of death. The cumulative coefficient shows how this effect accumulates over time.

  • Treatment (trt): A positive or negative time-varying coefficient for the treatment group indicates whether the test treatment increases or decreases the hazard of death compared to the standard treatment.

  • Time-Varying Effects: If the coefficients for certain covariates change over time, it means their effects on survival are not constant, which might suggest that the effect of these covariates varies depending on how long a patient has survived.

Summary and Conclusions

The Aalen additive hazards model is a flexible tool in survival analysis, allowing for time-varying effects of covariates on the hazard function. It provides an alternative to the Cox model, particularly when the assumption of proportional hazards does not hold. While the model’s interpretability may be more complex than the Cox model, it is a valuable tool for exploring time-dependent relationships in survival data.

References

  1. Aalen, O.O. (1989). A linear regression model for the analysis of life times. Statistics in Medicine, 8:907-925.
  2. Aalen, O.O (1993). Further results on the non-parametric linear model in survival analysis. Statistics in Medicine. 12:1569-1588.
  3. Survival Analysis with R