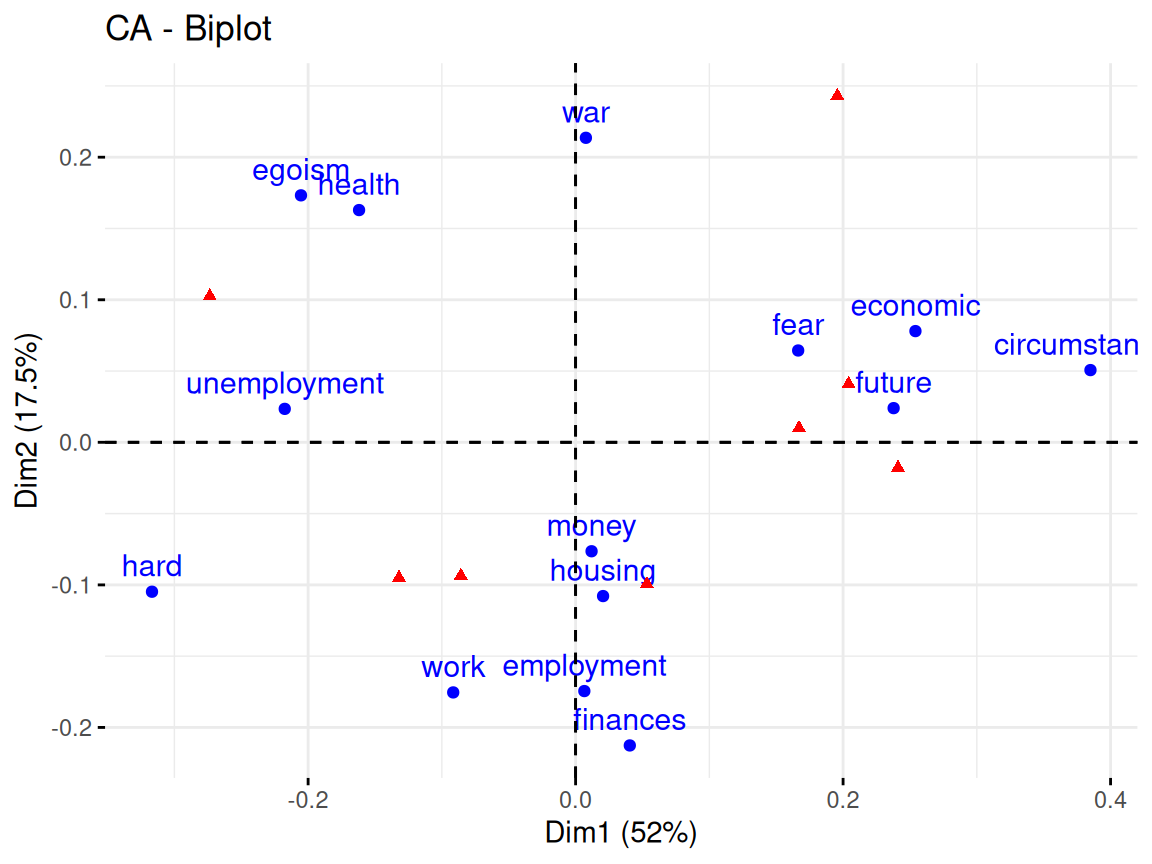
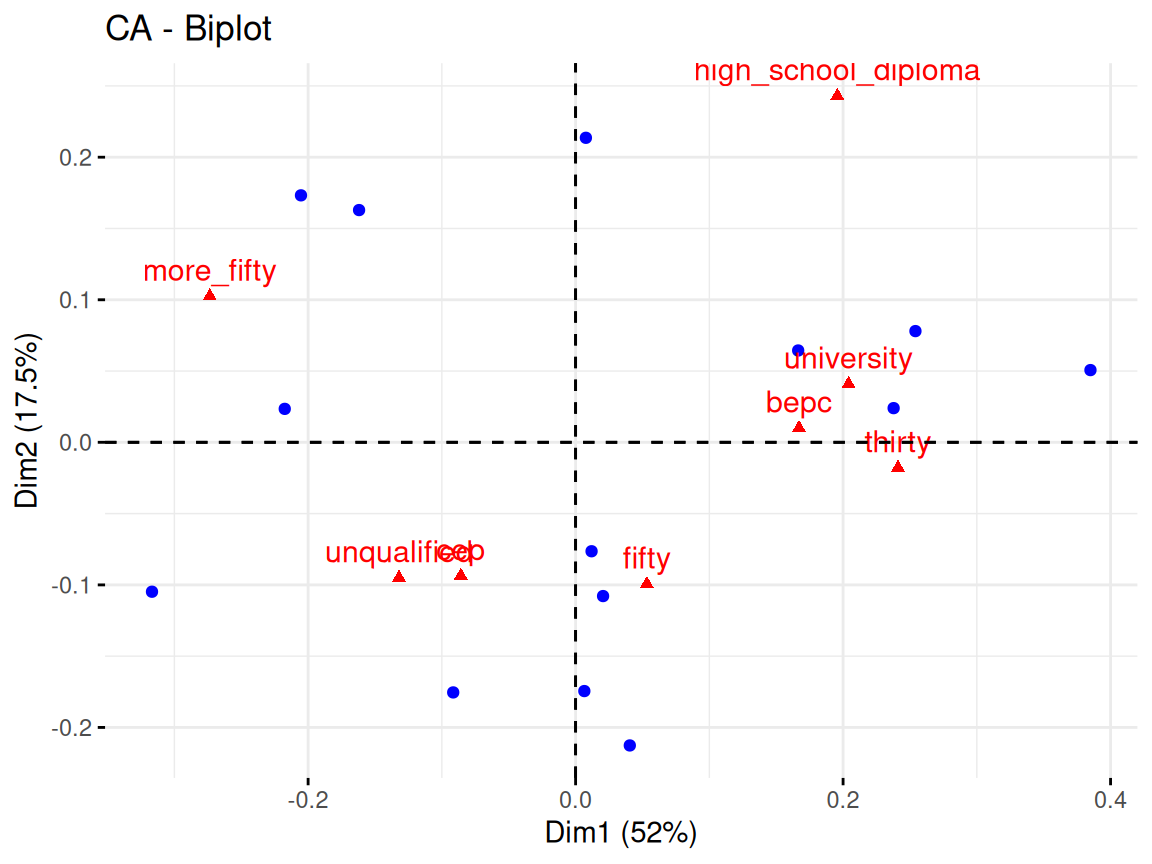
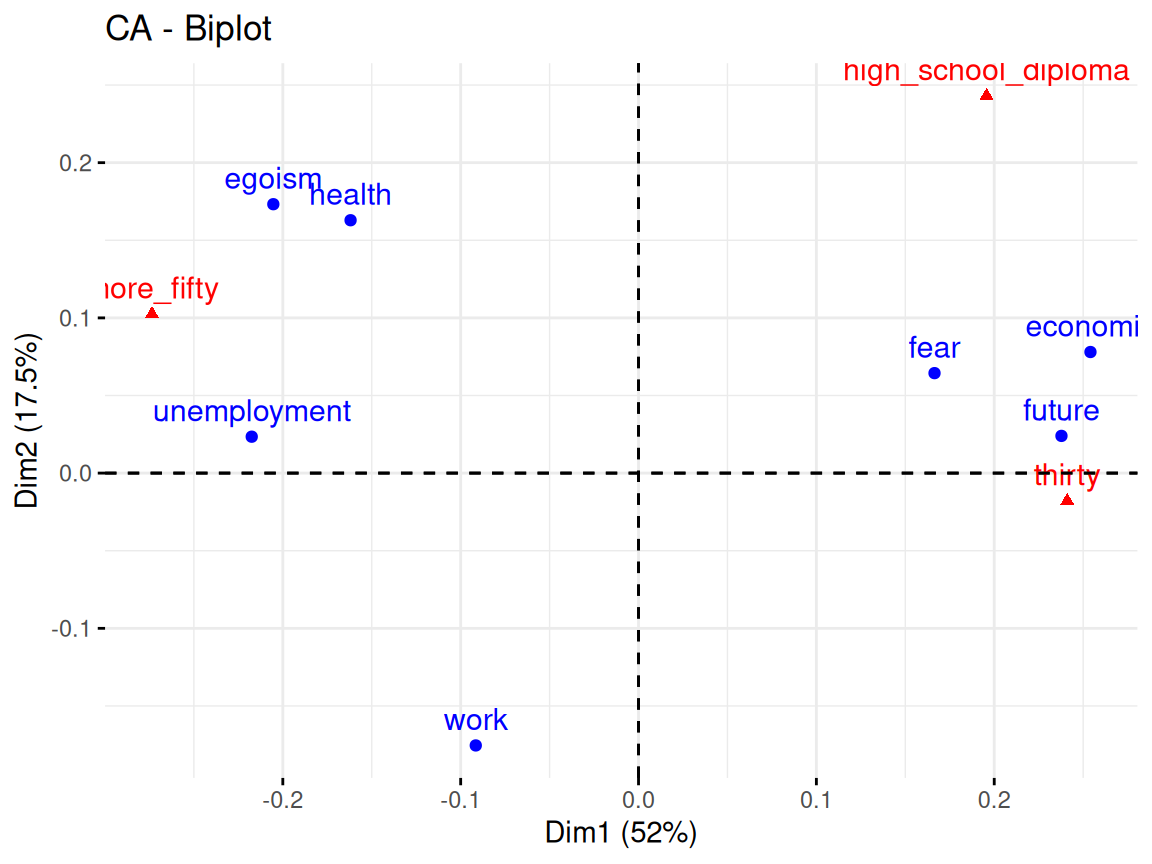
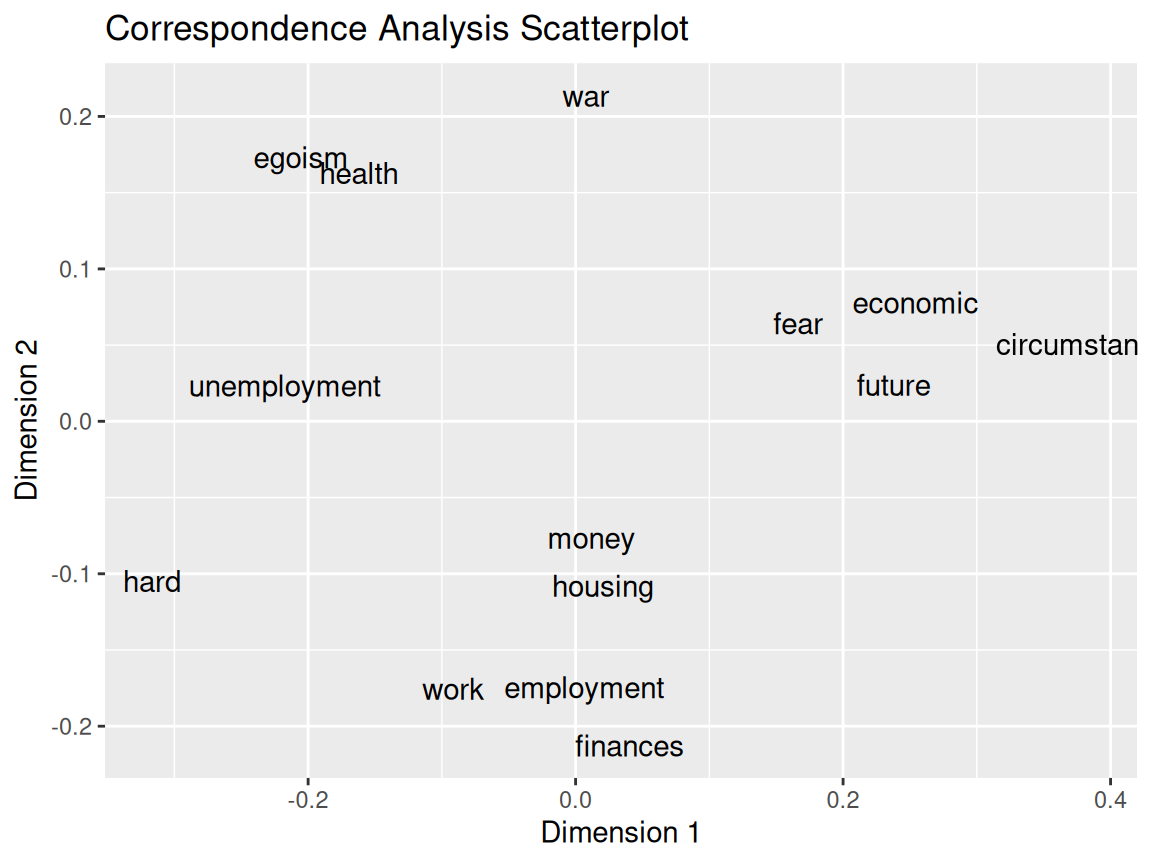
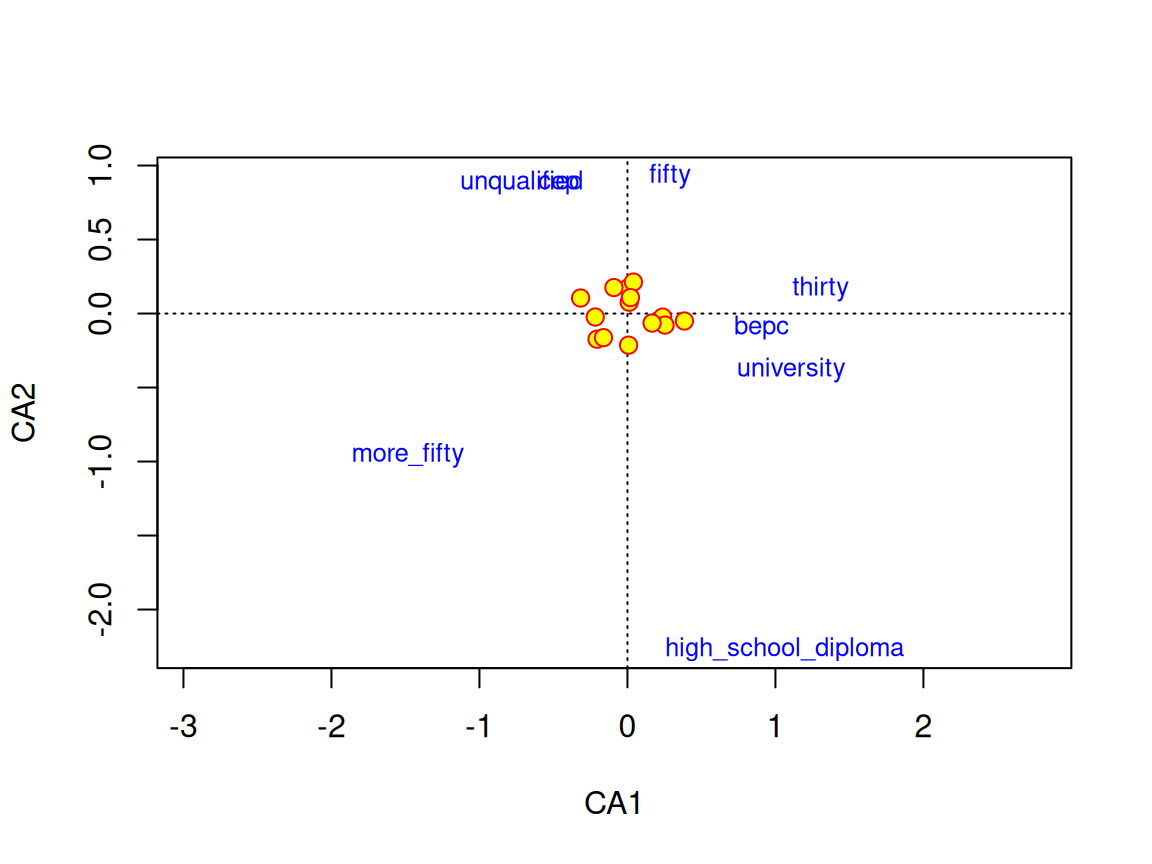
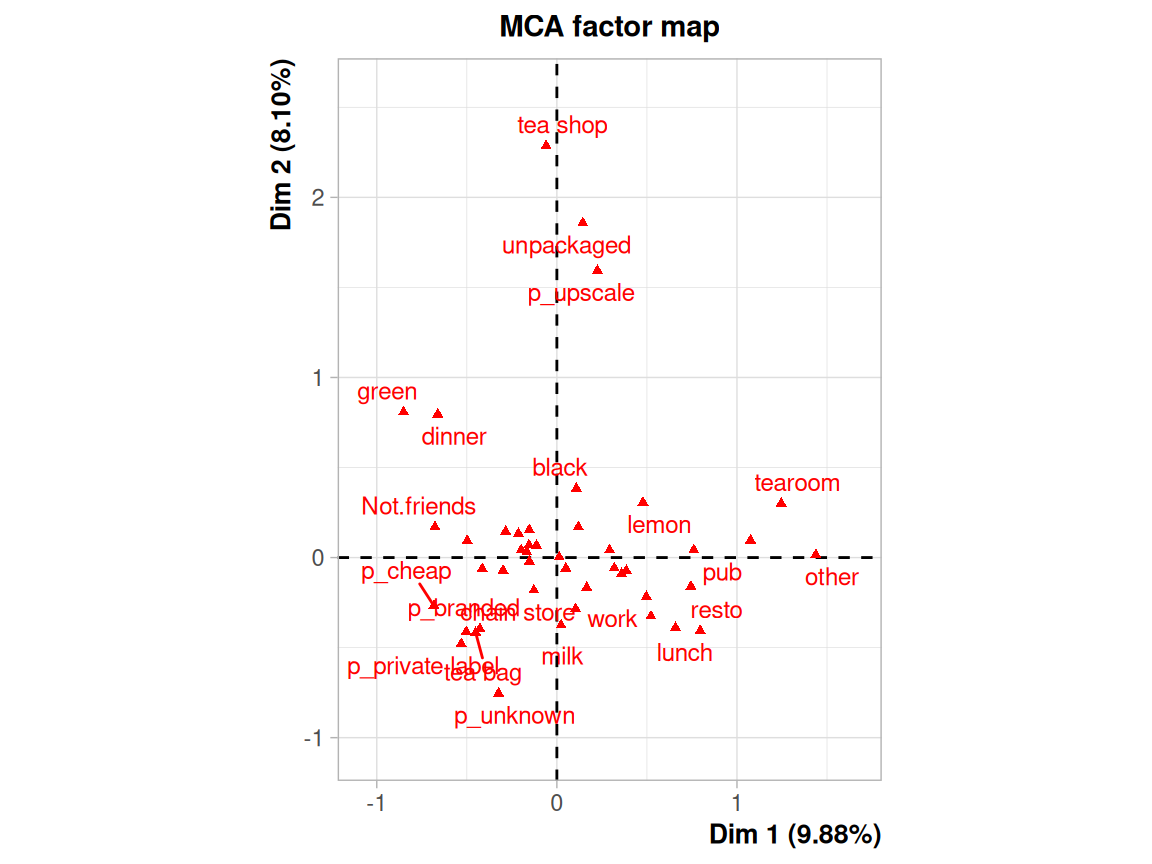
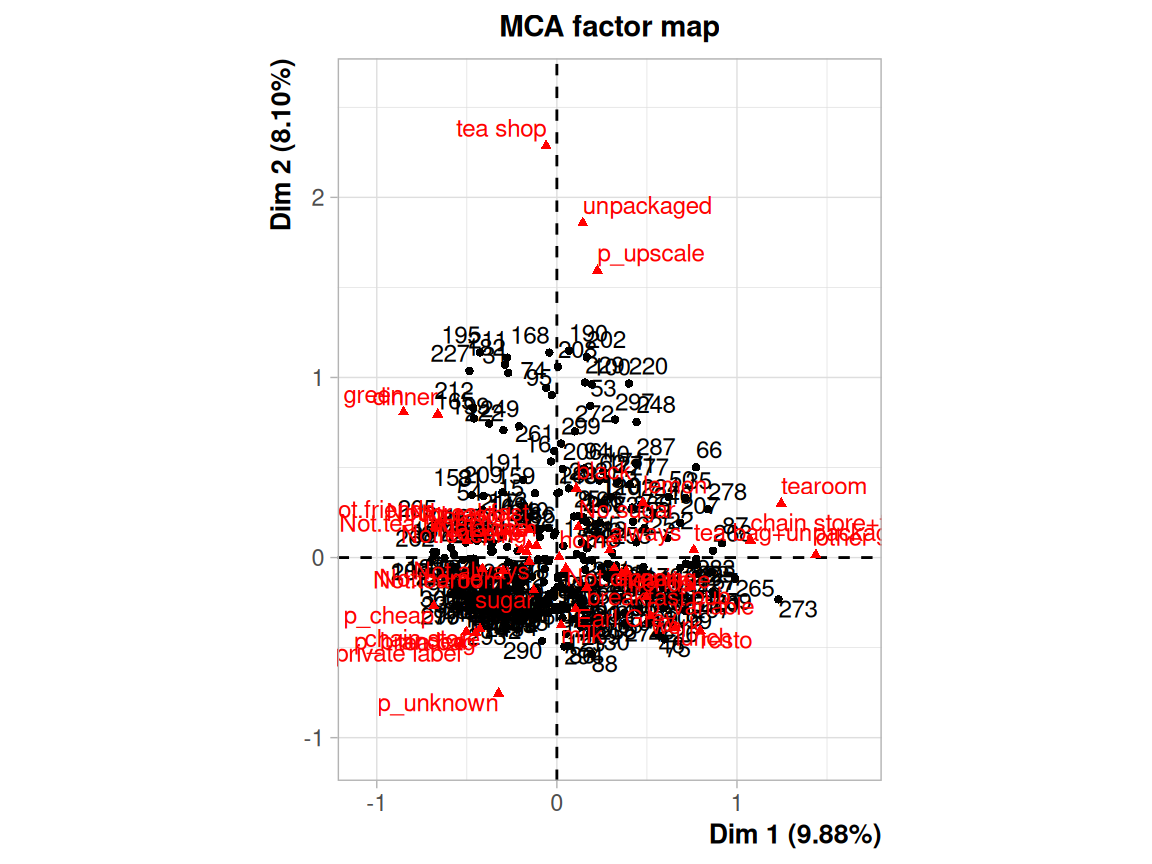
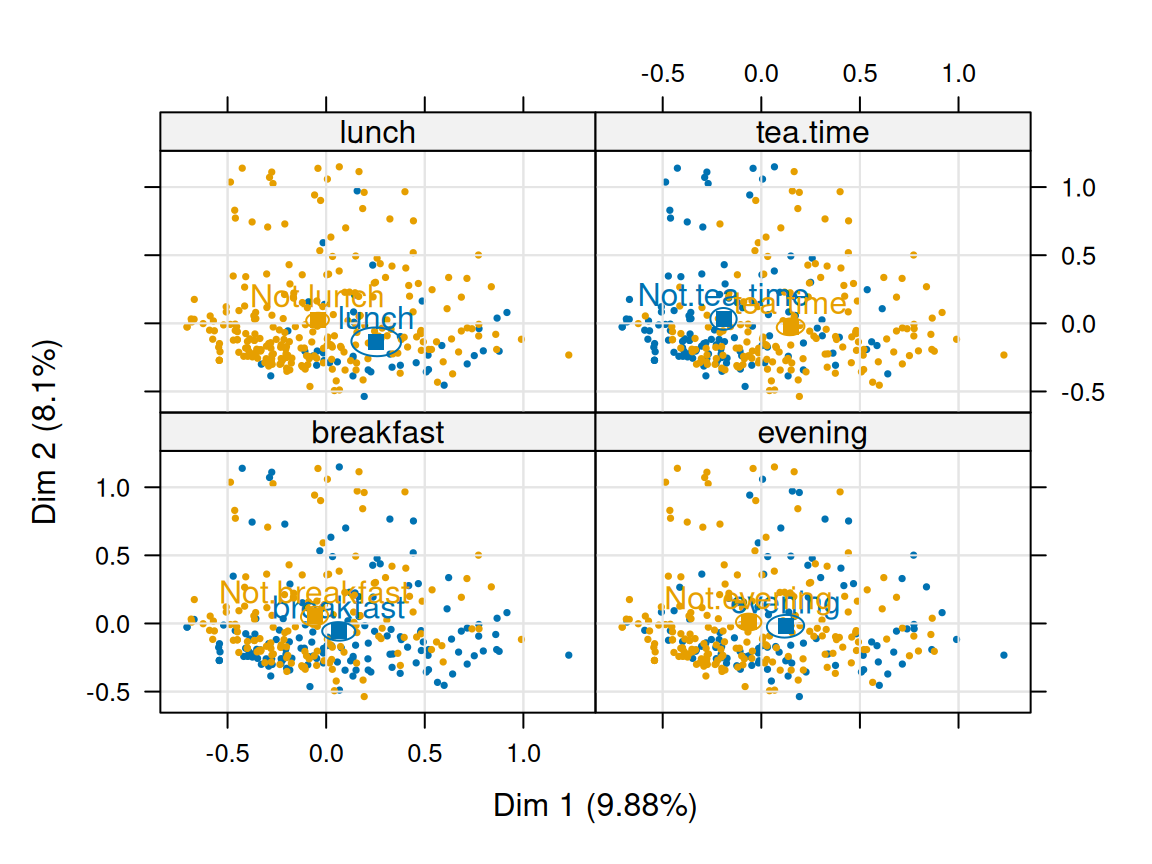
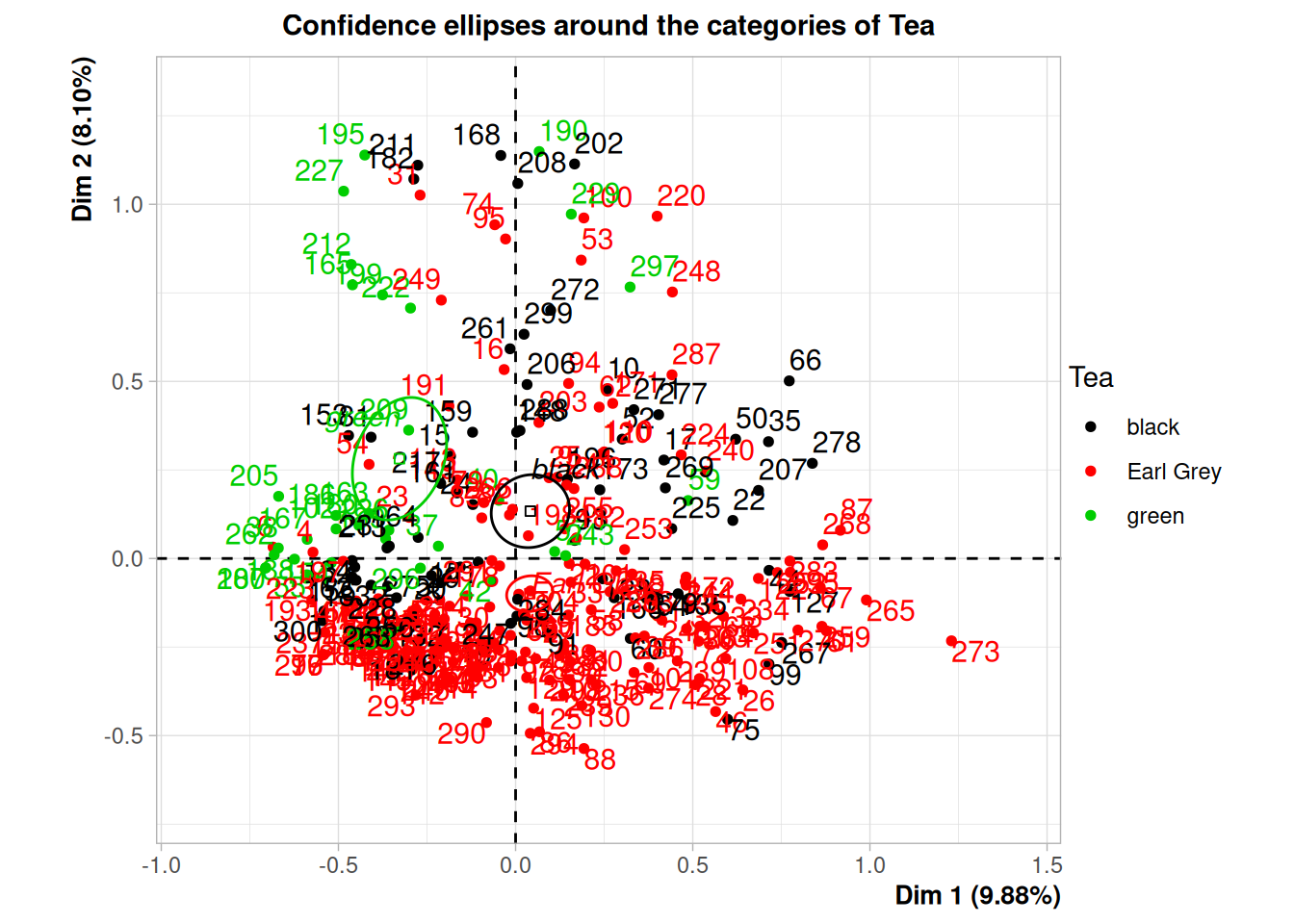
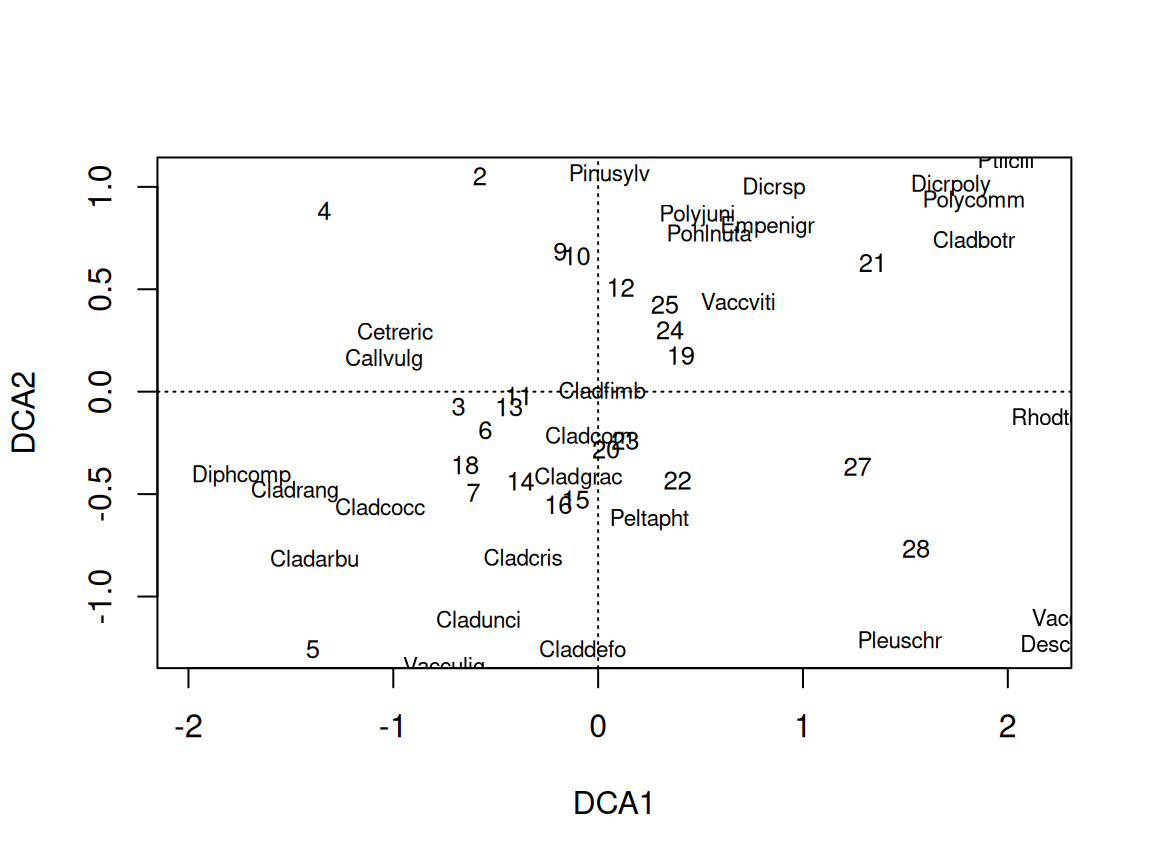
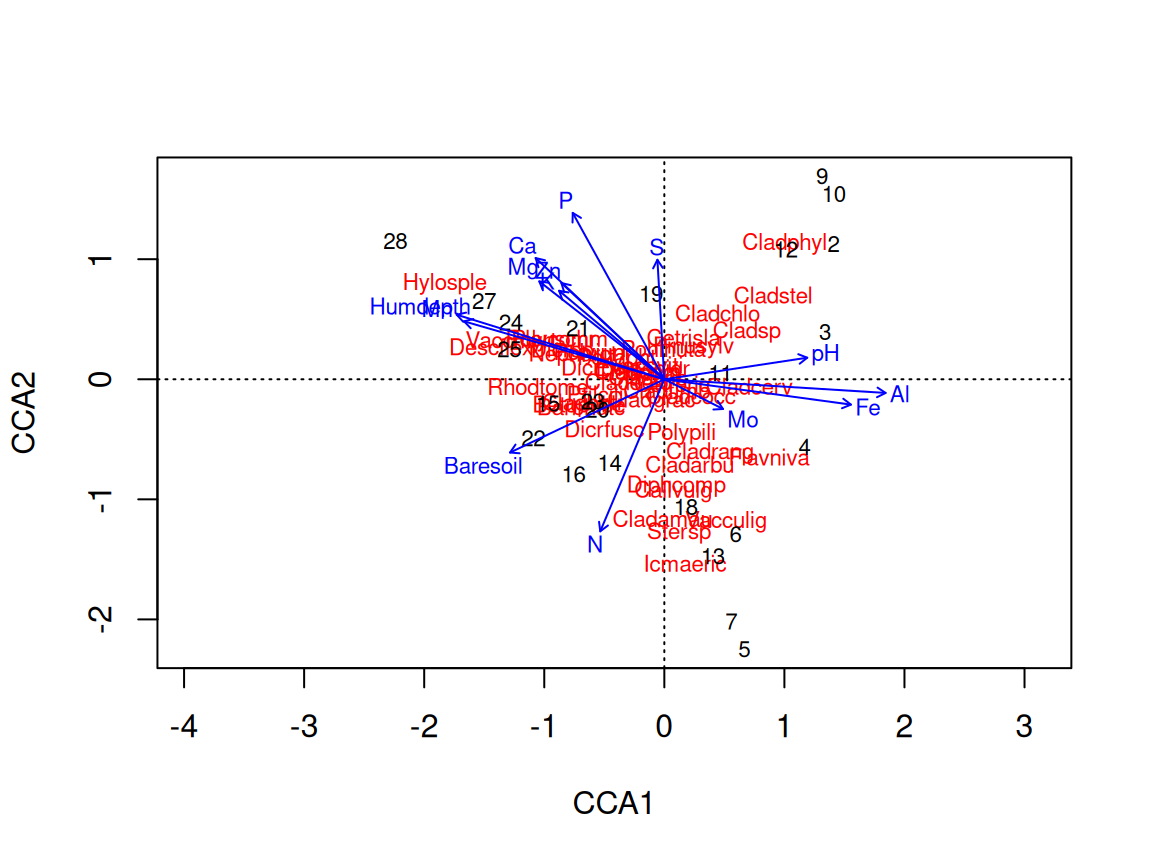
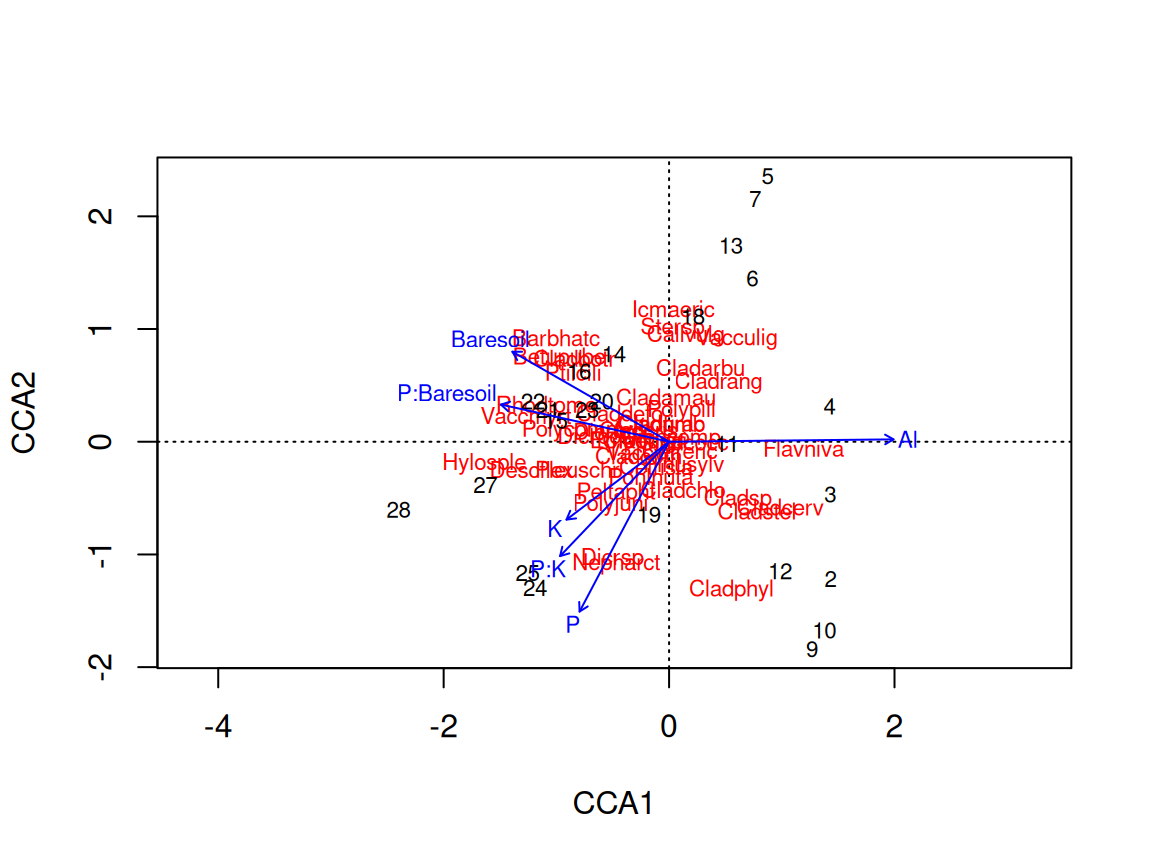
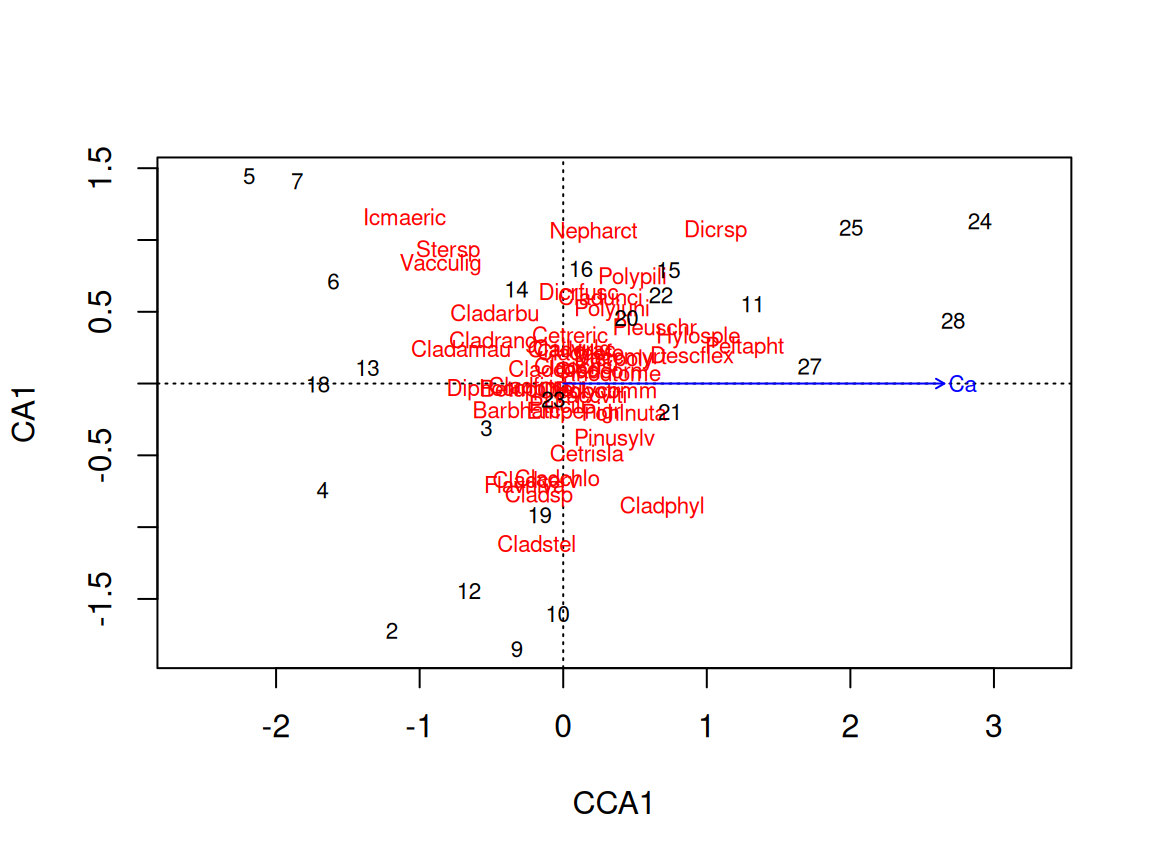
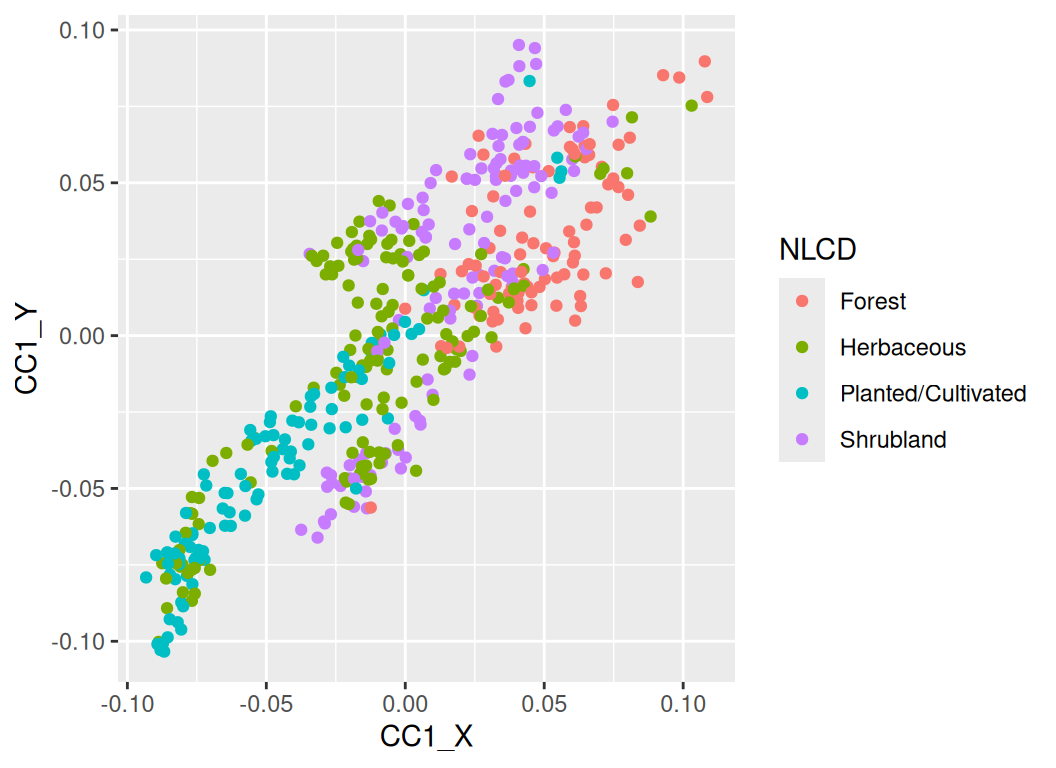
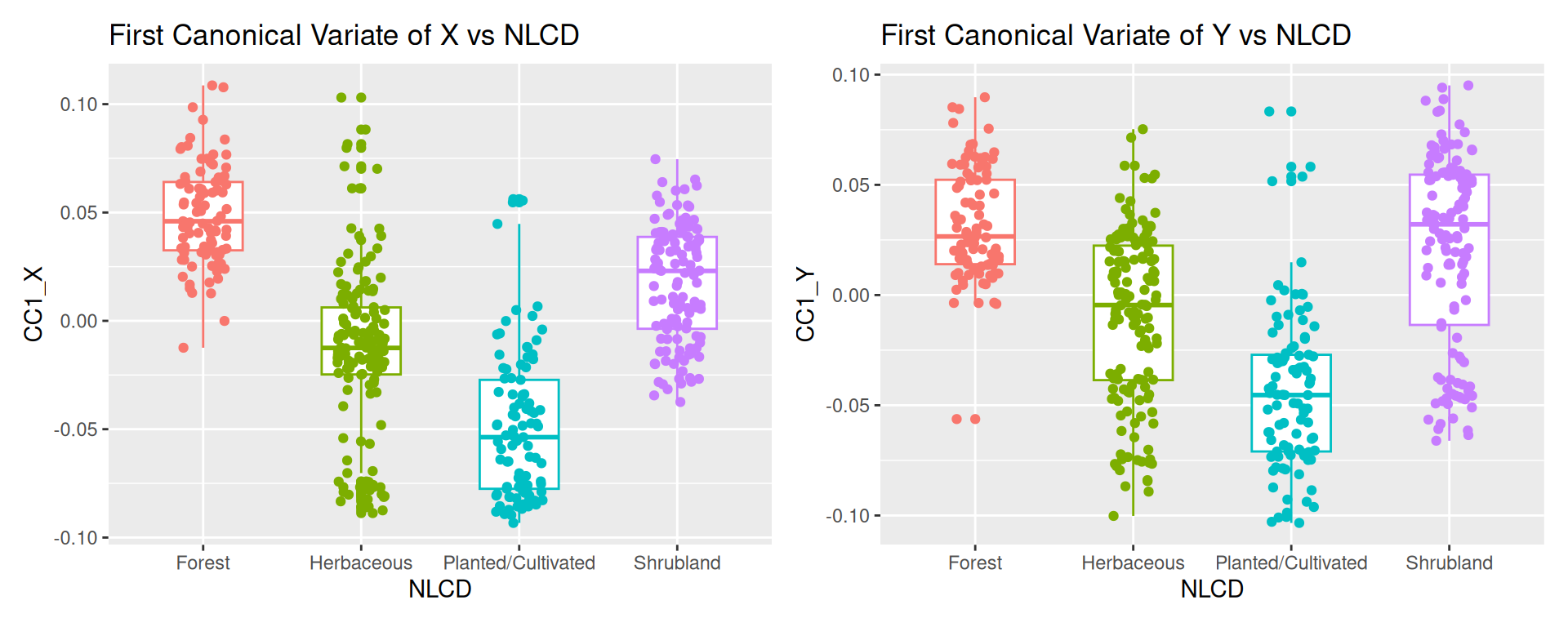
Rows: 24
Columns: 44
$ Callvulg <dbl> 0.55, 0.67, 0.10, 0.00, 0.00, 0.00, 4.73, 4.47, 0.00, 24.13, …
$ Empenigr <dbl> 11.13, 0.17, 1.55, 15.13, 12.68, 8.92, 5.12, 7.33, 1.63, 1.90…
$ Rhodtome <dbl> 0.00, 0.00, 0.00, 2.42, 0.00, 0.00, 1.55, 0.00, 0.35, 0.07, 0…
$ Vaccmyrt <dbl> 0.00, 0.35, 0.00, 5.92, 0.00, 2.42, 6.05, 2.15, 18.27, 0.22, …
$ Vaccviti <dbl> 17.80, 12.13, 13.47, 15.97, 23.73, 10.28, 12.40, 4.33, 7.13, …
$ Pinusylv <dbl> 0.07, 0.12, 0.25, 0.00, 0.03, 0.12, 0.10, 0.10, 0.05, 0.12, 0…
$ Descflex <dbl> 0.00, 0.00, 0.00, 3.70, 0.00, 0.02, 0.78, 0.00, 0.40, 0.00, 0…
$ Betupube <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.02, 0.00, 0.00, 0.00, 0…
$ Vacculig <dbl> 1.60, 0.00, 0.00, 1.12, 0.00, 0.00, 2.00, 0.00, 0.20, 0.00, 0…
$ Diphcomp <dbl> 2.07, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.07, 0…
$ Dicrsp <dbl> 0.00, 0.33, 23.43, 0.00, 0.00, 0.00, 0.03, 1.02, 0.30, 0.02, …
$ Dicrfusc <dbl> 1.62, 10.92, 0.00, 3.63, 3.42, 0.32, 37.07, 25.80, 0.52, 2.50…
$ Dicrpoly <dbl> 0.00, 0.02, 1.68, 0.00, 0.02, 0.02, 0.00, 0.23, 0.20, 0.00, 0…
$ Hylosple <dbl> 0.00, 0.00, 0.00, 6.70, 0.00, 0.00, 0.00, 0.00, 9.97, 0.00, 0…
$ Pleuschr <dbl> 4.67, 37.75, 32.92, 58.07, 19.42, 21.03, 26.38, 18.98, 70.03,…
$ Polypili <dbl> 0.02, 0.02, 0.00, 0.00, 0.02, 0.02, 0.00, 0.00, 0.00, 0.00, 0…
$ Polyjuni <dbl> 0.13, 0.23, 0.23, 0.00, 2.12, 1.58, 0.00, 0.02, 0.08, 0.02, 0…
$ Polycomm <dbl> 0.00, 0.00, 0.00, 0.13, 0.00, 0.18, 0.00, 0.00, 0.00, 0.00, 0…
$ Pohlnuta <dbl> 0.13, 0.03, 0.32, 0.02, 0.17, 0.07, 0.10, 0.13, 0.07, 0.03, 0…
$ Ptilcili <dbl> 0.12, 0.02, 0.03, 0.08, 1.80, 0.27, 0.03, 0.10, 0.03, 0.25, 0…
$ Barbhatc <dbl> 0.00, 0.00, 0.00, 0.08, 0.02, 0.02, 0.00, 0.00, 0.00, 0.07, 0…
$ Cladarbu <dbl> 21.73, 12.05, 3.58, 1.42, 9.08, 7.23, 6.10, 7.13, 0.17, 23.07…
$ Cladrang <dbl> 21.47, 8.13, 5.52, 7.63, 9.22, 4.95, 3.60, 14.03, 0.87, 23.67…
$ Cladstel <dbl> 3.50, 0.18, 0.07, 2.55, 0.05, 22.08, 0.23, 0.02, 0.00, 11.90,…
$ Cladunci <dbl> 0.30, 2.65, 8.93, 0.15, 0.73, 0.25, 2.38, 0.82, 0.05, 0.95, 2…
$ Cladcocc <dbl> 0.18, 0.13, 0.00, 0.00, 0.08, 0.10, 0.17, 0.15, 0.02, 0.17, 0…
$ Cladcorn <dbl> 0.23, 0.18, 0.20, 0.38, 1.42, 0.25, 0.13, 0.05, 0.03, 0.05, 0…
$ Cladgrac <dbl> 0.25, 0.23, 0.48, 0.12, 0.50, 0.18, 0.18, 0.22, 0.07, 0.23, 0…
$ Cladfimb <dbl> 0.25, 0.25, 0.00, 0.10, 0.17, 0.10, 0.20, 0.22, 0.10, 0.18, 0…
$ Cladcris <dbl> 0.23, 1.23, 0.07, 0.03, 1.78, 0.12, 0.20, 0.17, 0.02, 0.57, 0…
$ Cladchlo <dbl> 0.00, 0.00, 0.10, 0.00, 0.05, 0.05, 0.02, 0.00, 0.00, 0.02, 0…
$ Cladbotr <dbl> 0.00, 0.00, 0.02, 0.02, 0.05, 0.02, 0.00, 0.00, 0.02, 0.07, 0…
$ Cladamau <dbl> 0.08, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
$ Cladsp <dbl> 0.02, 0.00, 0.00, 0.02, 0.00, 0.00, 0.02, 0.02, 0.00, 0.07, 0…
$ Cetreric <dbl> 0.02, 0.15, 0.78, 0.00, 0.00, 0.00, 0.02, 0.18, 0.00, 0.18, 0…
$ Cetrisla <dbl> 0.00, 0.03, 0.12, 0.00, 0.00, 0.00, 0.00, 0.08, 0.02, 0.02, 0…
$ Flavniva <dbl> 0.12, 0.00, 0.00, 0.00, 0.02, 0.02, 0.00, 0.00, 0.00, 0.00, 0…
$ Nepharct <dbl> 0.02, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
$ Stersp <dbl> 0.62, 0.85, 0.03, 0.00, 1.58, 0.28, 0.00, 0.03, 0.02, 0.03, 0…
$ Peltapht <dbl> 0.02, 0.00, 0.00, 0.07, 0.33, 0.00, 0.00, 0.00, 0.00, 0.02, 0…
$ Icmaeric <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.07, 0.00, 0.00, 0…
$ Cladcerv <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…
$ Claddefo <dbl> 0.25, 1.00, 0.33, 0.15, 1.97, 0.37, 0.15, 0.67, 0.08, 0.47, 1…
$ Cladphyl <dbl> 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0…